本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
什么是循环神经网络?循环神经网络可以解决什么问题?
鱼离不开__?下意识的预测出可能性最大的字——“水”。这是因为人大脑中存在记忆,能够将鱼和水联系在一起。
循环核

- 循环核:参数时间共享,循环层提取时间信息。
- 循环核具有记忆力,圆柱体是记忆体,记忆体下面、侧面、上面分别有三组待训练的参数矩阵。通过不同时刻的参数共享,实现了对时间序列的信息提取。可以设定记忆体的个数以改变记忆体的容量。
解释上面的公式:
- $y_{t}$是当前时刻循环核的输出特征;$h_{t}$是每个时刻的状态信息;by是偏置;softmax为激活函数。
- $𝑥_{𝑡}$为当前时刻的输入特征;$ℎ_{𝑡−1}$为记忆体上一时刻存储的状态信息;bh为偏置;tanh为激活函数。
反向传播时:三个参数矩阵wxh、whh、why被梯度下降法更新。
前向传播时:记忆体内存储的状态信息ht,在每个时刻都被刷新,三个参数矩阵wxh、whh、why自始至终都是固定不变的。
循环核时间步展开
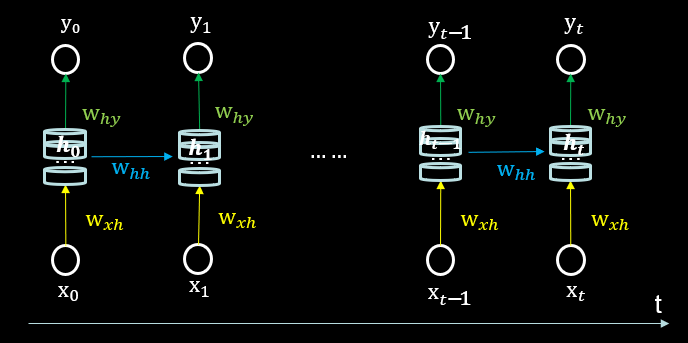
将循环核按时间步展开就是把循环核按照时间轴方向展开,可以得到上图。每个时刻的状态信息$h_{𝑡}$将会被更新,但记忆体周围的参数矩阵和两个偏置项是固定不变的,我们最终要得到的、训练优化的是这些参数矩阵。训练完成后,使用效果最好的参数矩阵执行前向传播,然后输出预测结果。这些参数矩阵就像我们人脑中成年累月累积下来的记忆数据,在遇到鱼离不开__?的时候,能够经过前向传播得到结论是“水”。
$y_{t}$就是神经网络的末层。从公式上来看$t_{t}$就是一个全连接的神经网络。借助全连接网络实现预测,
循环核计算层
每个循环核构成一层循环计算层,循环计算层的层数是向输出方向增长的。

有几个循环核就构成了几个循环计算层。
通过字母预测的例子:体会循环网络的手动计算过程
本小节通过手动计算循环计算层的前向传播体会一个字母预测的例子。
字母预测:输入a预测出b,输入b预测出c,输入c预测出d,输入d预测出e,输入e预测出a。
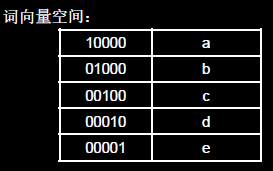
使用独热码对五个字母进行编码
因为神经网络的输入都是数字,所以我们先要把用到的a、b、c、d、e这五个字母用数字表示。最简单直接的方法就是用独热码对这五个字母编码。每个字母用一个独热码进行表示。(实际中可使用其他编码方式)
初始化wxh、whh和why三个参数矩阵
随机生成了Wxh、Whh和Why三个参数矩阵,记忆体的个数为3,初始状态ht为[0.0 0.0 0.0]

记忆体的个数选取3:

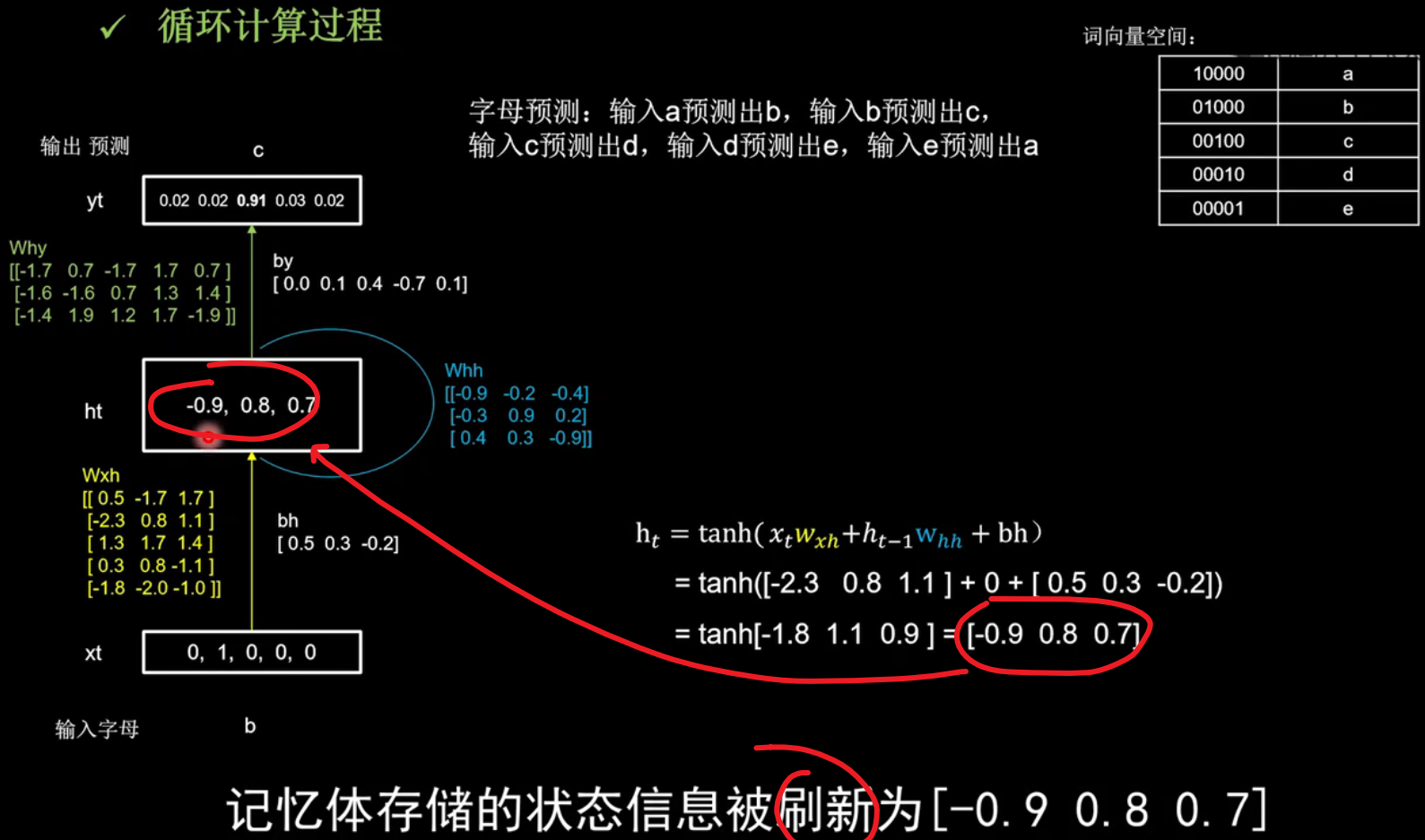
计算当前时刻的状态信息$h_{t}$
计算当前时刻的状态信息$h_{t}$如图右下角,开始计算。

经过tanh()函数后,记忆体$h_{t}$被刷新得到ht:
这一过程就是脑中的记忆被当前输入新的的事物更新了。
$$\begin{aligned} \mathrm{h}_{t} &=\tanh \left(x_{t} w_{x h}+h_{t-1} \mathrm{w}_{h h}+\mathrm{bh}\right) \\ &=\tanh ([-2.3 \quad 0.8 \quad 1.1]+0+[0.5\quad0.3\quad-0.2]) \\ &=\tanh [-1.8 \quad 1.1 \quad 0.9]=[-0.9 \quad 0.8 \quad 0.7] \end{aligned} $$

输出yt是把提取到的时间信息,通过全连接进行识别预测的过程,是整个网络的输出层,ht是当前记忆体内的数值[-0.9 0. 8 0. 7],乘以这个绿色的参数矩阵why,加上偏置矩阵by,得到[-0.7 -0.5 3.3 0.0 -0.7],过softmax函数得到[0.02 0.02 0.91 0.03 0. 02],可见模型认为有91%的可能性输出字母c,所以循环网络输出了预测结果c。
$$\begin{aligned} \mathrm{y}_{t}=& \operatorname{softmax}\left(h_{t} w_{h y}+b y\right) \\ =& \operatorname{softmax}([-0.7\quad-0.6\quad2.9\quad0.7\quad-0.8]+[0.0 \quad 0.1 \quad 0.4 \quad-0.7\quad0.1]) \\ &=\operatorname{softmax}([-0.7 \quad- 0.5 \quad 3.3 \quad0.0\quad-0.7]) \\ &=[0.02 \quad 0.02 \quad 0.91 \quad 0.03 \quad 0.02] \end{aligned}$$
前向传播算出预测矩阵
这一步就是学习完成后预测的过程,通过前向传播来实现的。

接下来$y_{t}$是把提取到的时间信息通过全连接预测。
通过字母预测的例子:体会循环网络的TensorFlow计算过程
本节目标:学习循环神经网络,用RNN、LSTM、GRU实现连续数据的预测(以股票预测为例)。
代码部分:
训练计算过程Ⅱ
把时间核按时间步展开,连续输入多个字母预测下一个字母的例子,以连续输入四个字母预测下一个字母为例。说明循环核按时间展开后,循环计算过程。
仍然使用三个记忆体,初始时刻记忆体内的记忆是0,用一套训练好的参数矩阵,说明循环计算的前向传播过程,在这个过程中的每个时刻参数矩阵是固定的,记忆体会在每个时刻被更新。
- 在第1个时刻b的独热码[0, 1,0, 0, 0]输入,记忆体根据更新公式刷新为[-0.9 0.2 0.2]
- 在第2时刻c的独热码[0, 0,1,0, 0]输入,记忆体根据更新公式刷新为[0.8 1.0 0.8]
- 在第3时刻d的独热码[0, 0, 0, 1,0]输入,记忆体根据更新公式刷新为[0.6 0.5 -1.0]
- 在第4时刻e的独热码[0, 0, 0,0, 1]输入,记忆体根据更新公式刷新为[-1.0 -1.0 0.8]
这四个时间步中,所用到的参数矩阵wxh和偏置项bh数值是相同的,输出预测通过全连接完成,带入yt计算公式得到[0.71 0.14 0.10 0.05 0.00],说明有71%的可能是字母a。
观察输出结果,模型不仅成功预测出了下一个字母是a,从神经网络输出的概率可以发现,因为输入序列的最后一个字母是e,模型认为下一个字母还是e的可能性最小,可能性最大的是a,其次分别是b, c, d。
代码示例
Embedding编码
独热码的缺点:独热码的位宽要与词汇量一致,如果词汇量增大时,非常浪费资源。因此自然语言处理中,有专门一个方向在研究单词的编码,Embedding 是一种编码方法,用低维向量实现了编码,这种编码可以通过神经网络训练优化,能表达出单词间的相关性。
- 独热码:数据量大过于稀疏,映射之间是独立的,没有表现出关联性。
- Embedding编码:是一种单词编码方法,用低维向量实现了编码,这种编码通过神经网络训练优化,能表达出单词间的相关性。
Ps:在自然语言处理中,有专门的一个方向研究单词的编码。
Tensorflow中给出了Embedding实现编码的函数。所以不用我们自己实现。
tf.keras.layers.Embedding(词汇表大小,编码维度)
- 词汇表大小:一共要表示多少个单词。
- 编码维度:打算用几个数字表示一个单词。
例如:想表示1到100这100个自然数,词汇表大小就是100,每个自然数用三个数字表示,编码维度就是3,代码如下:
tf.keras.layers.Embedding(100, 3)
Embedding层对输入数据的维度也有要求,要求输入数据是二维的,第一维度告知送入几个样本,第二维度告知循环核时间展开步数。
Embedding编码改进 – 预测单个字母
用RNN实现输入一个字母,预测下一个字母,用Embedding编码替换独热码。
代码示例:
Embedding编码改进 – 多个字母预测单个字母
用RNN实现输入连续四个字母,预测下一个字母。
代码示例
LSTM – 老师授课PPT,我的接受过程
传统循环网络RNN可以通过记忆体实现短期记忆,进行连续数据的预测,但是当连续数据的序列变长时,会使展开时间步过长,在反向传播更新参数时,梯度要按照时间步连续相乘,会导致梯度消失。所以在1997年Hochreitere等人提出了长短记忆网络LSTM,通过门控单元改善了RNN长期依赖问题。

长短记忆网络中引入了三个门限,都是当前时刻的输入特征xt和上个时刻的短期记忆ht-1的函数,这三个公式中Wi、Wf和Wo是待训练参数矩阵,bi、bf和bo是待训练偏置项,都经过sigmoid激活函数,使广门限的范围在0到1之间
输入门(门限) $$i_{t}=\sigma\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right) $$ 遗忘门(门限)$$ f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) $$ 输出门(门限) $$o_{t}=\sigma\left(W_{o} \cdot\left[h_{t-1}, x_{t}\right]+b_{o}\right)$$引入了表征长期记忆的细胞态Ct,细胞态等于上个时刻的长期记忆乘以遗忘门,加上当前时刻归纳出的新知识乘以输入门
细胞态(长期记忆) $$C_{t}=f_{t} * C_{t-1}+i_{t} * \tilde{C}_{t}$$ 记忆体表示短期记忆,属于长期记忆的一部分,是细胞态过tanh激活函数乘以输出门门]的结果
记忆体(短期记忆) $$h_{t}=o_{t} * \tanh \left(C_{t}\right)$$ 引|入了等待存入长期记忆的候选态Ct波浪号,候选态表示归纳出的待存入细胞态的新知识,是当前时刻的输入特征xt,和上个时刻的短期记忆ht-1的函数,Wc是待训练参数矩阵,bc是待训练偏置项
候选态(归纳出新的知识) $$\tilde{c}{t}=\tanh \left(W{c \cdot}\left[h_{t-1}, \quad x_{t}\right]+b_{c}\right)$$ 理解LSTM计算过程:
通俗易懂的解释:
LSTM就是听课的过程,现在脑中记住的内容是本节课第1分钟到第45分钟的长期记忆Ct,长期记忆Ct由两部分组成,
一部分,是本节课第1分钟到第44分钟的内容,也就是上一时刻的长期记忆Ct-1,因为不可能一字不差的记住所有内容,会遗忘掉一些,所以上个时刻的长期记忆Ct-1要乘以遗忘门ft,这个乘积项表示留存在脑中的对过去的记忆。
另一部分,现在所讲的内容是新知识,是即将存入脑中的现在的记忆,现在的记忆由两部组成,一部分是现在正在讲的第45分钟内容,还有一部分是第44分钟的短期记忆留存,这是上一时刻的短期记忆ht-1,脑中将当前时刻的输入xt和上一时刻的短期记忆ht-1,归纳形成即将存入你脑中的现在的记忆Ct波浪号,现在的记忆Ct波浪号乘以输入门与过去的记忆一同存储为长期记忆。
当我们把这节课的内容讲给其他人时不可能一字不漏的讲出来,我们讲的是留存在脑中的长期记忆,经过输出门ot筛选后的内容,这就是记忆体的输出ht。
当有多层循环网络时,第二层循环网络的输入xt,就是第一层循环网络的输出ht,输入第二层网络的是第一层网络提取出的精华。
用TensorFlow实现