本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
为什么使用FP-growth?
FP是频繁模式的缩写。Apriori算法需要多次扫描数据,I/O是很大的瓶颈。为了解决这个问题,FP Tree算法(也称FP Growth算法)采用了一些技巧,无论多少数据,只需要扫描两次数据集,因此提高了算法运行的效率。

FP树
什么是FP树?
FP(Frequent Pattern),即频繁模式的缩写。所以FP树又叫做频繁模式树。
FP-growth算法是一种将数据存储在FP树这种数据结构的算法,并可以直接从该数据结构中提取出频繁项集。
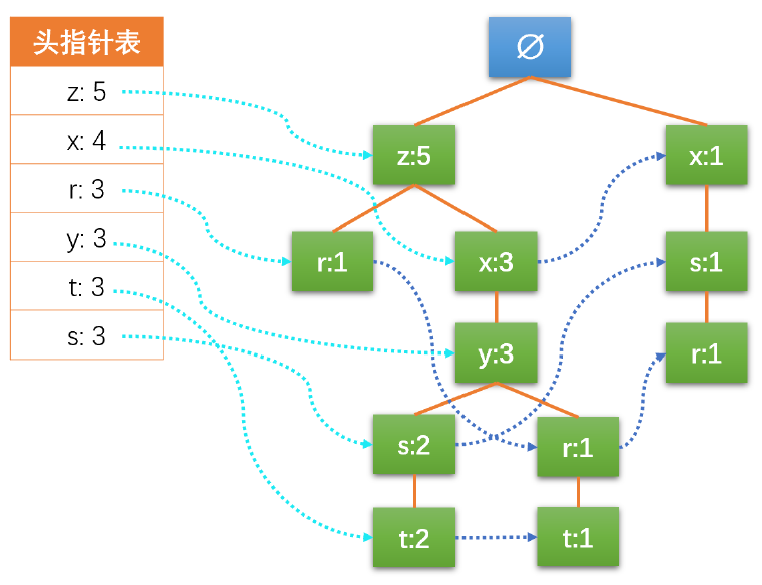
一棵FP树的结构如下图所示:

FP树的特点介绍:
- 空集作为跟结点。
- 每个结点由一个字母(这个字母是项名称):一个数字表示,数字表示项的频数。
- 一条路径(实线)表示的是一个事务,路径不同代表事物不同,所以一棵树中允许出现多个同名项。
- 如果事务完全一致,则路径可以重合。
- 相似项之间的链接(虚线)为节点链接(link),主要是用来快速发现相似项的位置。
为了快速访问树中的相同项,还需要维护一个连接相同项的节点的指针列表(headTable),每个列表元素(headTable的列)包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
算法步骤
题目来源书 P161页。
P161页。
下表中的TID表示订单号,商品ID是商品的唯一标识。

题目告知我们最小支持度为2。
第一步:扫描每个商品项出现的次数。
对题目中每一项进行扫描,统计在所有订单中出现的总次数。

对于小于最小支持度的项(<2),去除。本题中没有小于最小支持度的项。
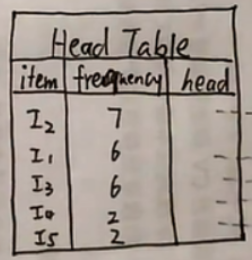
第二步:写出F-List;排序;重新构建表格
写出F-List:
![]()
排序:
次数多的排在前面。
![]()
因为有些项因为不满足最小支持度,会被删除掉。接下来还需要更新原始表格。
在本题中,没有项被删除,所以表格与原始表格相同,我们照抄下来。
铅笔是排序后的结果,根据每个项出现的频数降序排序。
eg:T100订单,I2的频数7>I1的频数6>I5的频数2。

第三步:画FP树
画出Head Table:
第一列式项名,第二类是出现的频数,第三类头结点。
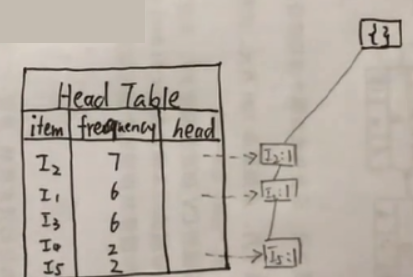
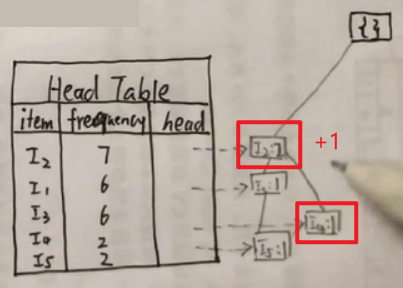
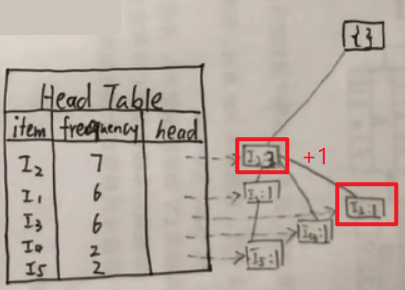
… …以此类推
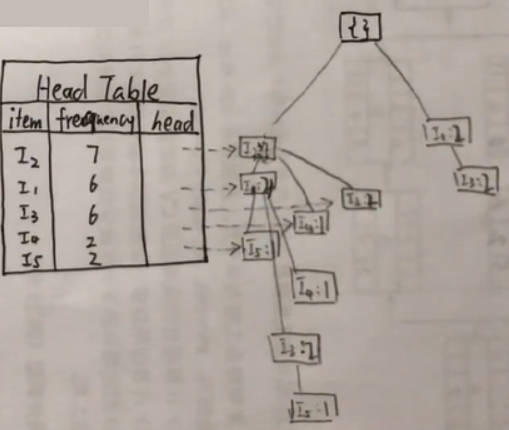
最后用虚线把相同的项连接起来:
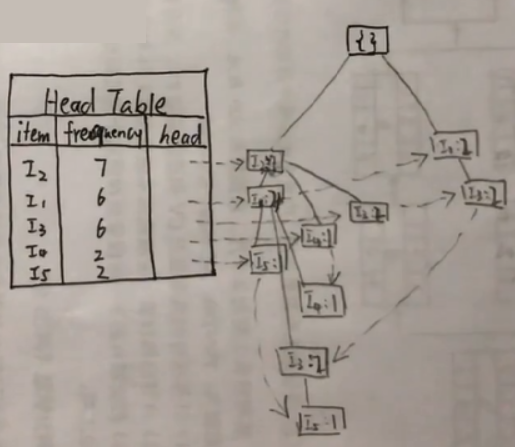
现在FP树就构造完成了。
第四步:列出表格,从FP树中抽取频繁项集
频繁项集表一共有4列。分别是项、条件模式集、条件频数和频繁项集。
- 项:Head Table item列第一个不要,剩下的倒叙写。
- 条件模式基。
方法:以I5项为例,在FP树中找到I5项,I5出现了两次,所以是有两个路径的,顺着路径往上找,有多个路径的算多个条件模式基。最后倒着写。I2, I1:1后面的数字代表的意思是这条路径走了1次。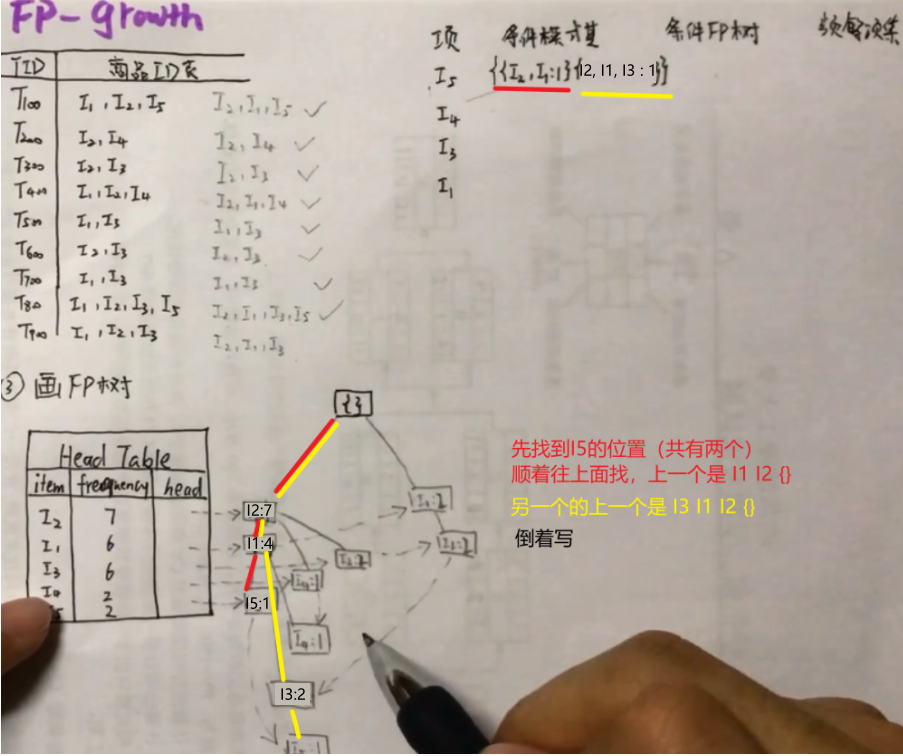

- 由条件模式基写条件FP:
方法:以I5项的条件模式基为例,第一个模式基I2出现了1次,I1出现1次;第二个模式基I2、I1、I3分别出现1次。共计I2出现2次,I1出现2次,I3出现1次。小于最小支持度的I3被舍丢弃。所以条件FP树为<I1:2, I1:2>。剩下的项以此类推… …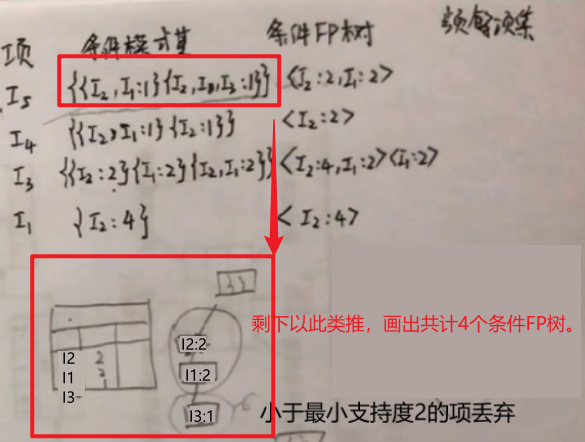
- 频繁项集:
方法:由项和条件FP树组合得到频繁项集。
例如第一个项I5与条件FP树<I2:2, I1:2>,I5可与I2、I5与I1,I5与I2和I1组合;
I4只能与自己的频繁FP树<I2:2>组合得到{I4, I2:2};
I3可与I2、I3与I1、I3与I2和I1;
I1与I2;
编码实现
源代码:FP-growth算法
参考文献:
https://www.bilibili.com/video/BV1fX4y1A75f