本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
现在我们已经学会了变换,剩下的问题是需要找到一组合适的基。
目标优化思路:找到一组最合适的基
去除平均值:减少计算量
PCA的最终目的是降维,得到前N个特征。所以数据本身的值并不是“很重要”。
我们为了减少计算量,将所有特征(每列)的均值变为0,达到减轻计算的目的。
举个例子,就好像我们要计算5个人成绩的离散程度,也就是方差,他们成绩分别是 100、98、102、99、101、100。他们的平均值是100分,我们直接去均值化,每个人都减去100分,处理后的分数是 0、-2、2、-1、1、0,现在计算方差是不是就方便许多。虽然分数变成个位数了对学生来说天壤差别,但是对我们来说并不关心平均值,而是关心数据的离散程度,并不影响。
计算协方差矩阵
补充知识:方差与协方差在PCA中的用途
问:提取最有价值的信息?
答:![]()
那么分散如何用数学来表示?——方差
关于方差、协方差、协方差矩阵忘记的同学可以简单回顾下:数理统计:方差、协方差、协方差矩阵与相关系数

目标:要找一个轴,使得数据在这个轴上方差是最大的。
假设均值为0时,协方差如下:
![]()
问:为什么要假设均值为0?
答:其实这是一种数据的预处理,叫做去中心化,是一种减轻计算量的方法,可看文章最开始的部分。
推广开:如果我们要提取两个特征,那么就是让方差最大的轴作为主轴,方差次大的轴就是次轴。一次类推,需要提取多少特征就是按照方差降序排序。
但多个特征之间希望是不相关的,而协方差就可以用来衡量两个或两个以上数据间的独立性、相关性。

问:为什么要保证是不相关,完全独立的?
答:其实我们不单单是这里希望特征之间不相关,在数据预处理中我们也希望特征之间不相关。
举个例子,一张销售表,一列统计的是每天卖了多少元的东西,另一列是每天卖出多少角的东西,这两列存在着强相关关系,显然保留一列就可以了。
所以说,我们一直是希望特征之间不相关的,这是数据分析的人之常情。强相关数据是多余的。
总结下我们的目标问题:
- 第一个轴:方差最大的方向。
- 第二个轴:前提是必须是与第一个基正交的方向上,选择一个方差最大的。第三个轴也要与第一个基、第二个基都正交的前提下选择方差最大的。后面以此类推… …
将目标问题通过数学来解决:
如何得到这些包含最大差异性的主成分方向呢?
答:通过计算数据矩阵的协方差矩阵,再计算协方差矩阵的特征值和特征向量
总体来说,接下来:
- 计算数据矩阵的协方差矩阵。
- 得到协方差矩阵的特征值及特征向量,选择特征值最大(也即包含方差最大)的N个特征所对应的特征向量组成的矩阵。
- 将数据矩阵转换到新的空间当中。

协方差矩阵的正对角线表示方差,负对角线表示两特征之间的关系。
eg:
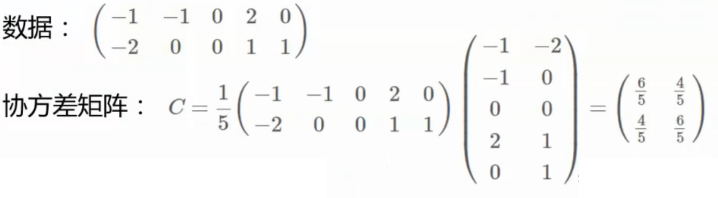
然后对协方差矩阵进行矩阵分解,得到特征值和特征向量。
eg:

将协方差矩阵对角化:用数学特征处理我们的目标问题
为什么要对角化?——对角化后两两元素之间的协方差为0,通过这一数学特征将我们的目标问题转化为数学目标问题。
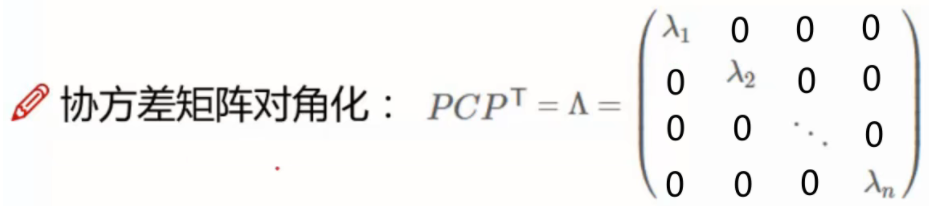
补充知识:如何对角化
特征向量可以使得协方差矩阵变成对角阵,实对称矩阵可以帮助我们对角化。

eg:

$P=\begin{pmatrix}
1& -1\\
1& 1
\end{pmatrix}$

将特征值从大到小排列并保留N个特征值
![]()
将数据转换到N个特征向量组成的新空间中
基乘以原始数据得到当前降维后的结果。
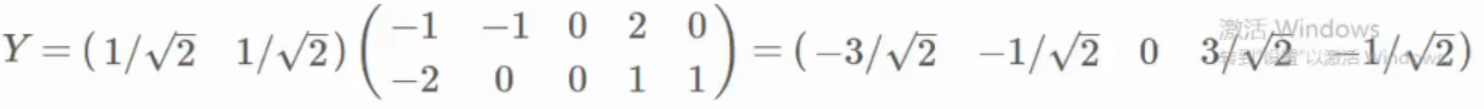
Python实现
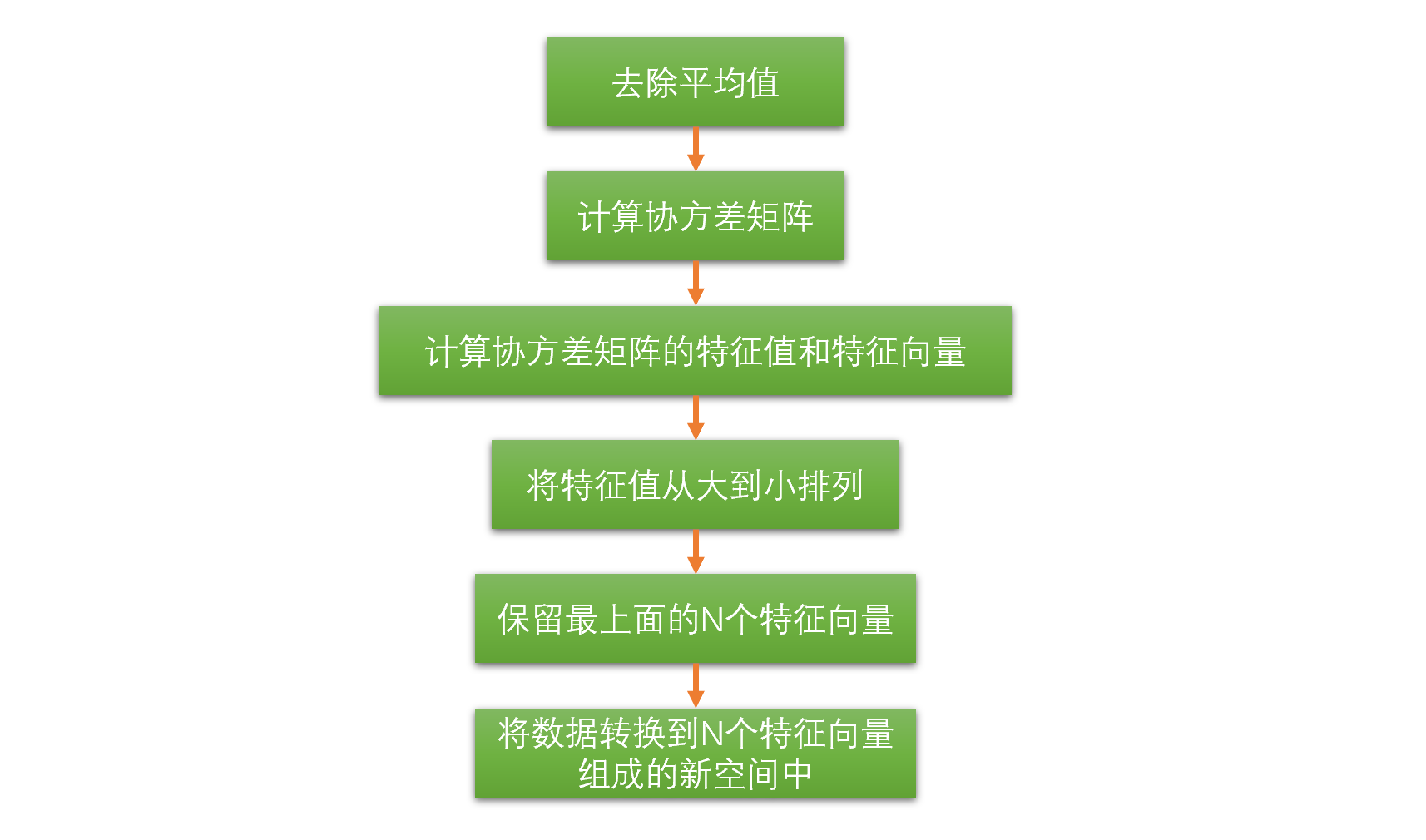
总结降维流程,为后续编码实现理清思路:
方差的分母为什么是n-1?
为了得到样本方差的无偏估计。(详细去看数学书)
代码下载
Python代码演示:PCA
代码源文件&数据源:降维算法
PCA使用方差作为信息量的衡量指标;SVD使用奇异值分解来找出空间V。
需要注意的是,主成分分析得出来的主成分很难通过一些现实的意义来解答,可依据主成分进行分类。如果在意因果关系与可解释性可用因子分析。
参考文献:
https://www.bilibili.com/video/BV1Zt41187bN(没讲原理,只有python实现)
https://www.bilibili.com/video/BV1PJ411G74g(讲了原理,没有代码)