本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
前序文章:集成算法
Bagging算法(英语:Bootstrap aggregating,引导聚集算法),又称装袋算法,是机器学习领域的一种集成学习算法。
如何生成多个臭皮匠?
本质是放回式采样。
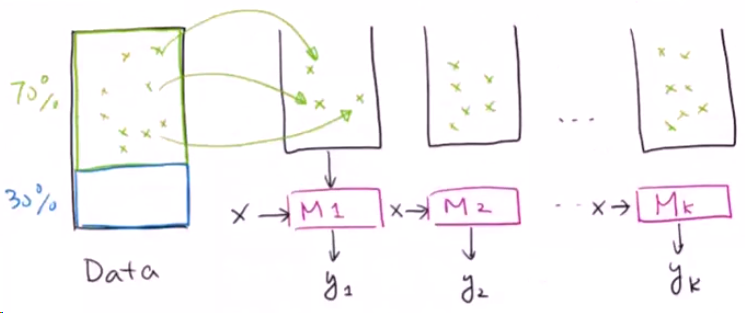
现在我们有一组数据,其中70%是训练数据,剩下的30%是测试数据。测试数据是为了验证我们模型的正确率的,我们在实现模型的时候不能碰。那么我们从70%的训练数据入手。
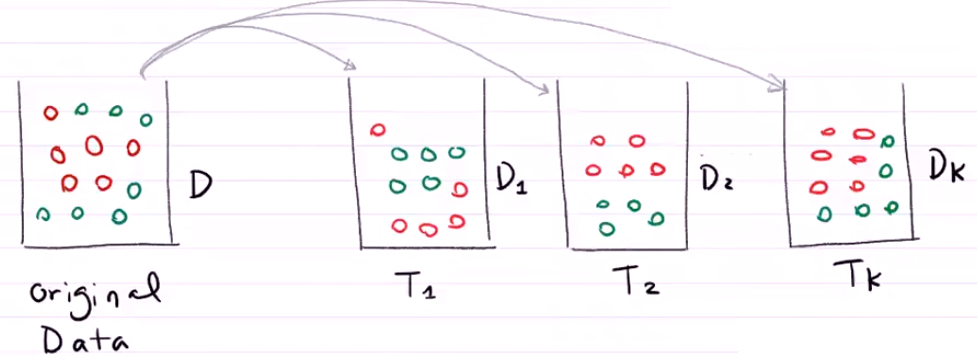
首先,我们将数据进行放回式采样。从70%的训练集中随机取出一个小球将其放入到第一个篮子M1中,然后将其放回Data的70%训练集中。下一步再从训练集中随机取出一个小球将其放入到第二个篮子M2中,然后同样的将小球放回… … 以此类推。我们得到了k个篮子。
我们现在得到了新的若干个篮子。
为什么要重复采样?——让数据变得更清晰
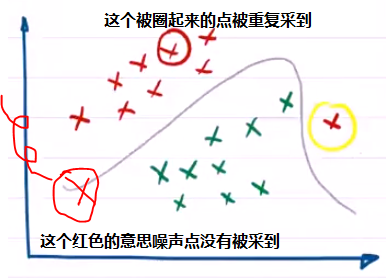
加入我们的原始数据Data长这个样子:这个图看起来似乎有点怪,它的左下角和右上角以及右下角黄色圆圈的点,这三个点显得不是那么和谐。他们会不会是噪声点呢?
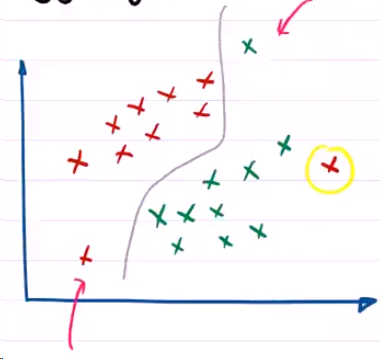
如果我们进行了一个重复采样,可能就会得到下面的一个篮子,有些噪声可能就不会被采到了:
如果再次采集,奇怪的噪声可能就会没有了:
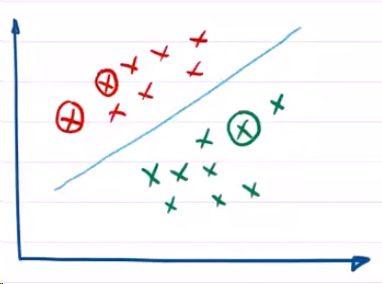
通过这样的重复采集,我们可以知道原始的数据Data可能并不是一个很复杂的,东拐西拐弯的数据,他可能就是一个简单的聚集在一堆的红叉叉和绿色的叉叉。
质量不够,数量来凑——使用多个臭皮匠
我们以决策树方法为例,我们现在拥有三个决策树,他们是由不同的数据点得到的三棵树。
现在这个新的模型与之前的不同,它拥有三颗决策树,与之前的一棵决策树不同,现在进进来一个数据需要做分类,我们在使用这个模型的时候可以让三颗决策树进行投票。例如第一颗决策树T1认为新来的数据应该是红色,第二颗树也认为是红色,而第三颗树说是绿色。红色和绿色的投票结果是2:1,少数服从多数,即最后我们输出的结果认为,这个新进来的数据应该被划分为红色。
总结:
- 原始数据通过不断的放回式采样得到三个决策树,这三个决策树(三个分类器)(臭皮匠)都对新加入的值做判断,最后投票决定到底这个数据是哪一类(诸葛亮)。另外我们还认为三个分类器的权重相同。
- 上面的图用到了Random Forest(随机森林)算法。
- Bagging最大的特点是可以并行处理数据,再不同的计算机上面分布式处理。
参考文献:
https://www.bilibili.com/video/BV1Sk4y1m7Dy?p=7