本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
前序课程
支持向量机学习路线,请学习本节软间隔最大化之前先看之前的硬间隔最大化。支持向量机:线性可分支持向量机与硬间隔最大化
软间隔优化:解决过于“严格”划分问题
软间隔:数据中的噪音。
之前的方法过于“严格”,我们要求所有点都分的对,先分的对,再要求间隔最大。而现在,我们认为这个要求不免过于严格,我们有时需要放松一点。——软间隔问题。
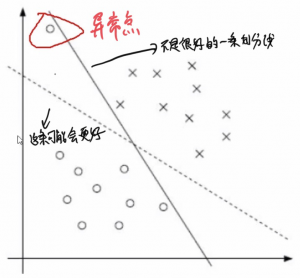
为了解决该问题,引入松弛因子。
![]()
Ps:$\xi _{i}$叫做松弛变量。
原来是$y_{i}(w\cdot x_{i}+b)>=1$,必须等于等于1,而现在可以对当前的样本$x_{i}$允许你进入到黄线区域内。
具体的松弛因子我们可以不用过于深度的了解,刚开始学习的时候我们先懂表面,后续随着学习的深入再逐渐深入了解关于松弛因子的问题。

核变换:解决低维不可分问题
左图,二维空间中的红点和蓝点,在二维平面上不是很好划分;而右图中我们通过升高维度,使用一个平面就可以轻易的划分红点和蓝点。
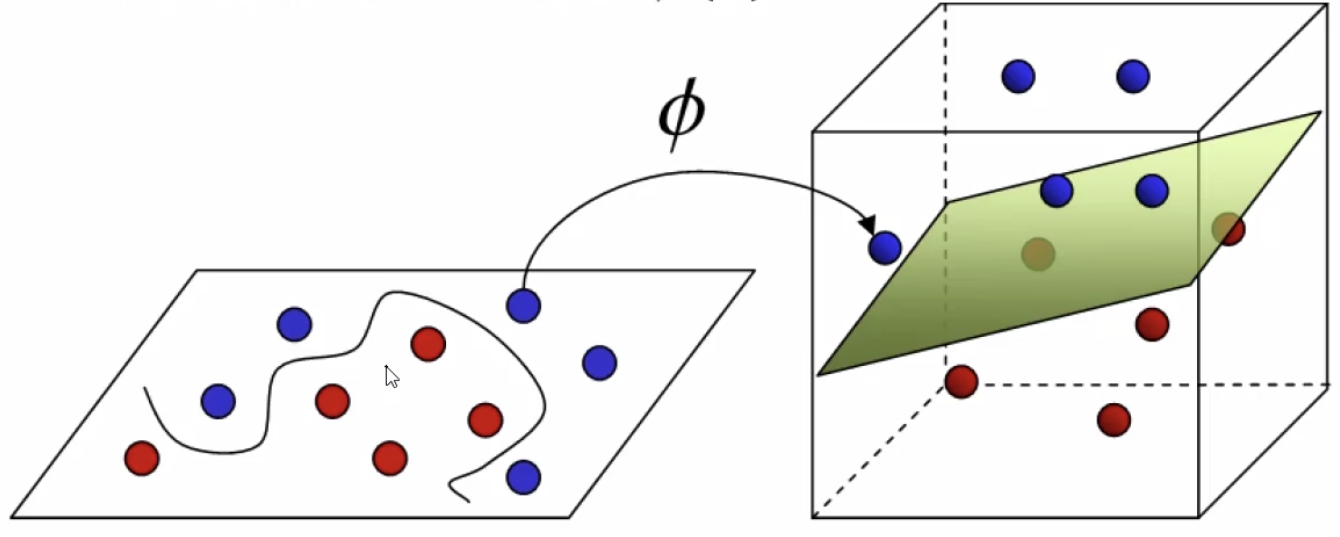
为什么可以升高维度?升到维度的本质是什么?
试想如果我跟王俊凯作比较,我们都有共同特征,例如我们都是男生、我们都是20多岁。但是我们也存在不同特征,例如我喜欢机器学习而王俊凯不一定喜欢、我不是明星而王俊凯是明星。那么如果我们以第一个维度(性别)去划分,显然就无法划分的开。如果我们升高维度(例如再加一个特征年龄),依然是无法划分的开。如果我们加到第三个特征(爱好),这样子,我就与王俊凯可分了。所以升高维度的本质就是增加一个特征。
回想决策树,我们也是根据信息增益来构造决策树的,也是以特征作为划分依据的。决策树生长的过程也是一个升高维度让数据变得可分的过程。决策树的树叶即我们想划分的样本点。
另一个问题解释为什么要升高纬度:

解决方法:

引入某种函数将数据点先做内积,再做映射(B式)。这样就可以避免先把数据映射到高维空间,然后在高维空间做内积产生大量的运算问题(A式)。

这种函数我们称为核函数。但是要注意,我们通过核函数可以知道减少运算的这种简便方法,并不是把数据点映射到高维空间中,只是借鉴了这种思想和巧合完成了这种简便预算。
只要升高维度就一定可分吗?会出现永远不可分的情况吗?
答:不会,只要我们升高维度到了一定程度,就一定可分。
例如上面我与王俊凯问题,因为我与王俊凯一样是不一样的两个人,一定是存在不同点的,所以升高的一定维度,特征增加到一定维度,我与王俊凯一定就变得可划分。
同样的,决策时通过筛选特征,一定会将某种特征有区别的两个或若干个样本点划分出来。
SVM核函数之一——高斯核函数:偷懒的办法,先做内积再做映射以升高纬度
真正在使用的时候:![]()
高斯核函数式SVM常用的核函数之一,但并是唯一。含有许多其他的核函数,例如多项式核函数、卡方核函数、余弦相似核函数等等。
序列最优最小化算法(SMO)
未完待续
参考文献:
https://www.bilibili.com/video/BV1UR4y147AT?p=9
https://www.bilibili.com/video/BV1i4411G7Xv?p=7