本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
感知机模型
感知机是一个二分类线性判别模型,假设输入$x\in \mathbb{R}^n$,输出$y\in\{-1,+1\}$,感知机为如下函数:
$f(x)=sign(w^Tx+b)$,
$\\sign(x)=\left\{\begin{aligned}
1 \qquad \quad x\ge0\\
-1 \qquad\quad x<0
\end{aligned}\right.$
其中,w叫做权重,是分类超平面的法向量;b叫做偏置,是超平面的截距。
通俗的来讲,我们希望机器构造出一条直线,将图中的红豆、绿豆划分开。这条线叫做超平面。同时将红豆视为正例(+1),绿豆视为反例(-1)。即确定感知机模型参数w和b。
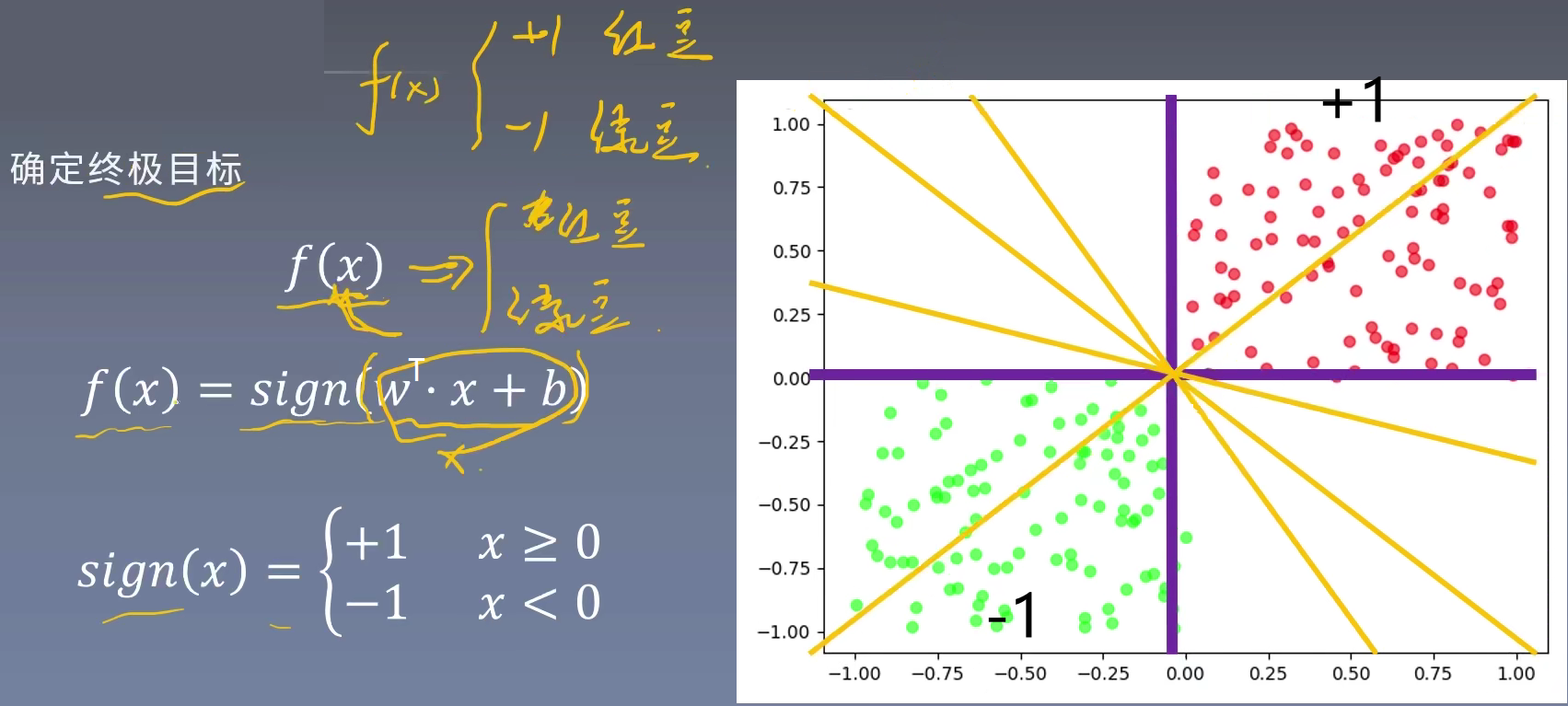
感知机学习策略
什么是线性可分
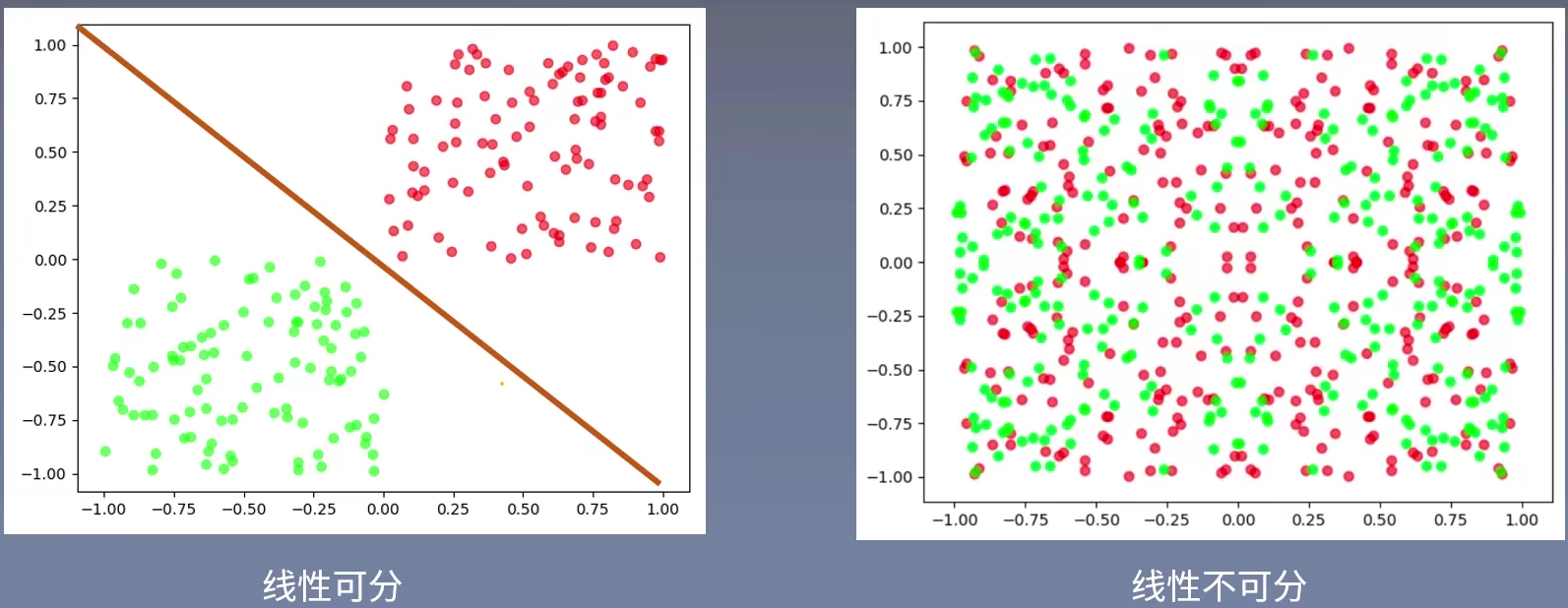
几何间隔与函数间隔

函数间隔
$\sum_{i=1}^{N} \left | w^{T} x_{i} + b \right | $
使用几何间隔
即我们传统的点到直线距离公式,下面这个公式代表图上所有点到直线距离之和。几何间隔表示的是点到超平面的距离:

上面图片里是我百度的点到直线的距离公式。其中,A和B的平方和的二次方跟就是上面函数间隔里的w的2-范数,绝对值里面的一堆其实就是函数间隔计算出来的值。也就是几何间隔等于函数间隔除以系数的2-范数。
对于其中一个错分类数据$(x_{i},y_{i} )$来说,这个点到超平面的公式为:
$-y_{i} (w^{T}x+b )>=0$
$y_{i} $代表标签,正例为+1,反例为-1。$w^{T}x_{i} +b$代表预测数结果,若$w^{T}x_{i} +b>0$代表预测为正例,<0代表预测是负例。如果是错误数据,则上述的公式一定是>=0的。
为什么感知机不使用函数间隔

使用函数间隔存在的问题:上面两张图,点到直线的距离发生了变化,他们的距离公式分别为:
$w^{T} x+b=1$
$\frac{1}{2}w^{T} x+\frac{1}{2}b=\frac{1}{2}$
第二张图会导致得出的w和b特别小。
如果使用几何间隔,假设有距离公式:$2w^{T} x+2b = 2$,那么空间中所有点到超平面的几何间距为:$\frac{1}{\left | \left | w \right | \right | } \left | w^{T} x+b \right | $,这里${\left | \left | w \right | \right | } $是w的L2范数。
$\frac{\left | 2w^{T} x+2b \right | }{\sqrt{\sum_{i=1}^{N}(2w^{T}_{i} )^{2} } } = \frac{2\left | w^{T}x+b \right | }{2\sqrt{\sum_{i=1}^{N}(w^{T})^{2} } }= \frac{\left | w^{T}x+b \right | }{\sqrt{\sum_{i=1}^{N}(w^{T})^{2} } }$
几何间隔就是函数间隔除以了w的模。使用二范数可以让距离变得不那么重要。——对超平面的法向量w加以一定的约束,如规范化。
由于感知机的前提是原数据集线性可分,这意味着必须存在一个正确的超平面。那么,不管几何距离还是函数距离,损失函数最后都要等于0,因此感知机并不关心点到超平面之间的间隔,关心的是误分类的点的个数。使用函数间隔并不会带来什么好处,反而会使学习过程复杂化。所以我们采用几何间隔即可满足需要。
函数间隔与几何间隔的关系:
所以一个误分类点到超平面的几何距离是:
$-\frac{1}{\left | \left | w \right | \right | } y_{i} (w^{T}x+b )$
所有误分类点到超平面的几何距离是:
$-\frac{1}{\left | \left | w \right | \right | } \sum_{x_{i}\in M }^{} y_{i} (w^{T}x+b )$
感知机的损失函数
设数据集线性可分,则感知机的损失函数为所有误分类点到分类超平面的函数间隔,即:
$L(w,b)=-\sum_{x_i\in M}y_i(w^Tx+b)$
其中M为所有误分类点的集合。并且L(w,b)函数一定是非负的,误分类点越少,误分类点离超平面越近,这个函数的值越接近0,直到没有误分类点则函数值为0。
感知机学习算法
感知机学习算法的原始形式
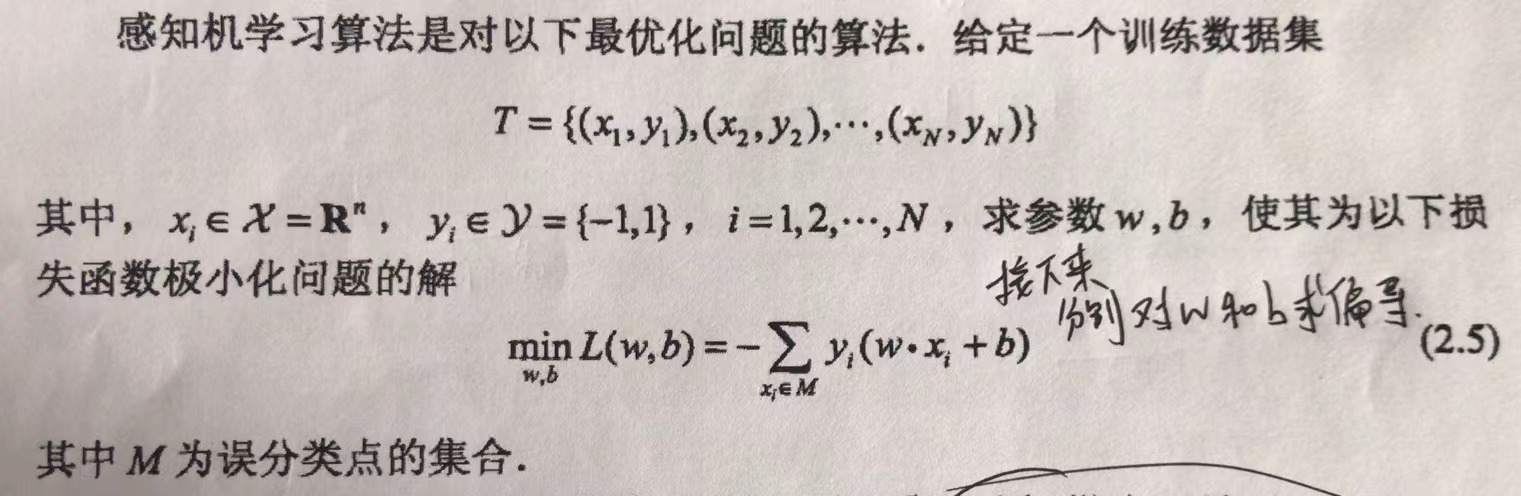
接下来分别为w和b求偏导,得到w和b的参数更新公式。

最终得到下述算法:
输入:训练数据集$T={(x_1,y_1),(x_2,y_2),..,(x_N,y_N)}$,其中$x_i\in \mathbb{R}^n$,$Y_i\in{-1,1}$;学习率$\eta\in(0,1]$
输出:w,b;感知机模型$f(x)=sign(w^Tx+b)$
-
随机任选一个超平面$w_0,b_0$,一般都初始化为0
-
在训练集中选取数据$(x_i,y_i)$
-
如果$y_i(w^Tx_i+b)\le 0$,则更新w和b:
$w_{i} =w_{i-1}+\eta y_ix_i$
$b_{i}=b_{i-1}+\eta y_i$ -
转至第二步,直到训练集中没有误分点
感知机学习算法的对偶形式(暂时跳过了)
对偶形式的基本想法是,将w和b表示为实例$x_i$和标签$y_i$的线性组合的形式,通过求解其系数而求得w和b。
由感知机算法的原始形式可以得出,修改n次过后w,b关于$(x_i,y_i)$的增量分别是$\alpha_iy_ix_i$和$\alpha_iy_i$,这里$\alpha_i=n_i\eta$。这样,最后学习到的w和b可以分别表示为:
$w=\sum_{i=1}^N\alpha_iy_ix_i\\b=\sum_{i=1}^N\alpha_iy_i$
具体算法为:
输入:训练数据集$T={(x_1,y_1),(x_2,y_2),..,(x_N,y_N)}$,其中$x_i\in \mathbb{R}^n$,$Y_i\in{-1,1}$;学习率$\eta\in(0,1]$
输出:$\alpha$,b;感知机模型$f(x)=sign(\sum_{i=1}^N\alpha_iy_ix_ix+b)$,其中$\alpha=(\alpha_1,\alpha_2,…,\alpha_N)^T$
-
令$\alpha=\boldsymbol 0, b=0$
-
在训练集中选取数据$(x_i,y_i)$
-
如果$y_i(\sum_{j=1}^N\alpha_jy_jx_jx_i+b)\le 0$,则更新w和b:
$\alpha=\alpha+\eta\\b=b+\eta y_i$
-
转至第二步,知道训练集中没有误分点
感知机算法的对偶形式主要适用于训练数据的特征维度远大于训练样本数的场景,此时原始形式每次更新都需要计算w和x的内积,但对偶形式可以将所有样本间的内积预先计算好以矩阵的形式存储(Gram矩阵),这样会节省训练耗时。
书中例子
图P29页 例2.1
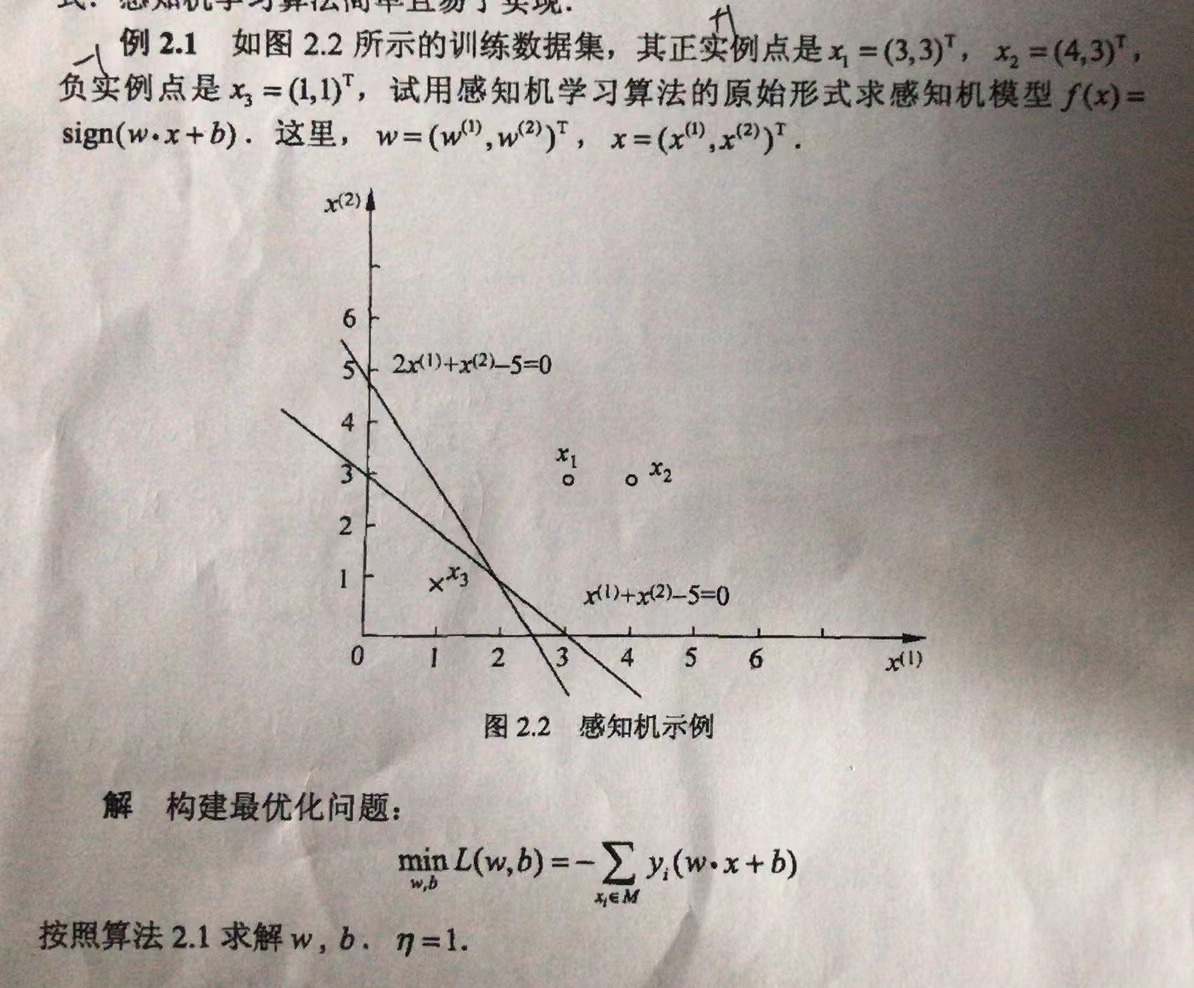
手解:

编程解:
import numpy as np
import matplotlib.pyplot as plt
class Perception():
'''
感知机算法,包括原始形式和对偶形式
'''
def __init__(self):
self.learing_rate = 1
def train(self, data, labels):
'''
原始形式的感知机算法,输入数据必须线性可分
:param data: (n*m),n为样本个数,m为特征个数
:param labels: 样本标签
'''
data_size = data.shape[0]
#初始化w,b
self.w = [0] * (data.shape[1])
self.b = 0
y_pred = np.sign((np.dot(data, self.w) + self.b))
#是否有误分类标记,当有误分类样本时执行以下循环
flag = (y_pred == labels).all()
while not flag:
for i in range(data_size):
y_pred = np.sign((np.dot(data, self.w) + self.b))
if y_pred[i]*labels[i] <= 0:
self.w += self.learing_rate * data[i] * labels[i]
self.b += self.learing_rate * labels[i]
print(self.w,self.b)
flag = (y_pred == labels).all()
def get_gram_matrix(self, data):
#计算格拉姆矩阵
data_size = data.shape[0]
gram_matrix = np.zeros((data_size, data_size))
for i in range(data_size):
for j in range(data_size):
gram_matrix[i, j] = np.dot(data[i], data[j])
self.gram_matrix = gram_matrix
def dual_output(self, x_index, data_size, labels):
'''
计算第x_index个样本的对偶形式的输出,这里不进行符号函数运算
:param x_index: 样本索引
:param data_size: 样本个数
:param labels: 样本标签
'''
output = self.b
for i in range(data_size):
output += (self.alpha[i] * labels[i] * self.gram_matrix[i, x_index])
return output
def train_dual(self, data, labels):
#d对偶形式的感知机算法
self.b = 0
self.get_gram_matrix(data)
data_size = data.shape[0]
self.alpha = [0] * data_size
flag = False
while not flag:
y_pred = [0] * data_size
for i in range(data_size):
y_pred[i] = np.sign(self.dual_output(i, data_size, labels))
if labels[i] * y_pred[i] <= 0:
self.alpha[i] += self.learing_rate
self.b += self.learing_rate * labels[i]
print(self.alpha,self.b)
flag = (y_pred == labels).all()
if __name__ == '__main__':
# data1中第一列表示x轴坐标;第二列代表y轴作表;第三列表示标签,1表示正例,-1代表反例。
data1 = np.array([[3, 3, 1], [4, 3, 1], [1, 1, -1]]) # 书中例题数据检验算法
# numpy切片:https://www.runoob.com/numpy/numpy-indexing-and-slicing.html
data = data1[..., 0:2]
labels = data1[..., -1]
model = Perception()
# 使用原始形式(还有一种对偶形式代码写了,但暂时不研究)
model.train(data, labels)
# 画图
# 轴范围 0~5
plt.xlim(0, 5)
plt.ylim(0, 5)
x = data1[..., 0]
y = data1[..., 1]
labl = data1[..., 2]
# 参考:https://www.codenong.com/12487060/
colors = ['red' if l == 1 else 'green' for l in labl]
plt.scatter(x, y, c=colors)
# python如何根据斜率和截距画直线?:https://www.3rxing.org/question/ca80d8505f642814980.html
print("model.w[0]:", model.w[0])
print("model.w[1]:", model.w[1])
print("model.b:", model.b)
k = - (model.w[0] / model.w[1])
print("斜率k:", k)
b = -model.b / model.w[1]
print("截距b:", b)
# 生成x的等差数列0-10之间取100个数
xx = np.linspace(0, 5, 100)
# 生成每个x对应的y
y = k * xx + b
# 画直线
plt.plot(xx, y)
plt.show()
# #随机生成数据,在y=x附近生成数据(暂时不做)
# x = np.linspace(0,50,50)
# y1 = x + np.random.randint(1,5,50)
# y2 = x + np.random.randint(-5,-1,50)
# data_positive = np.c_[x,y1]
# data_negative = np.c_[x,y2]
# labels_positive = np.ones(50)
# labels_negative = -np.ones(50)
# data = np.r_[data_positive,data_negative]
# labels = np.r_[labels_positive,labels_negative]
#
# model = Perception()
# model.train(data,labels)

参考文献:
《统计学习方法》李航
https://www.bilibili.com/video/BV1i4411G7Xv?p=2
https://github.com/1033020837/Basic4AI
https://ld246.com/article/1585574258471
