本文已收录于机器学习笔记系列，共计 20 篇，本篇是第 9 篇

本文已收录到：机器学习笔记专题

文章目录 隐藏

前序课程：集成方法

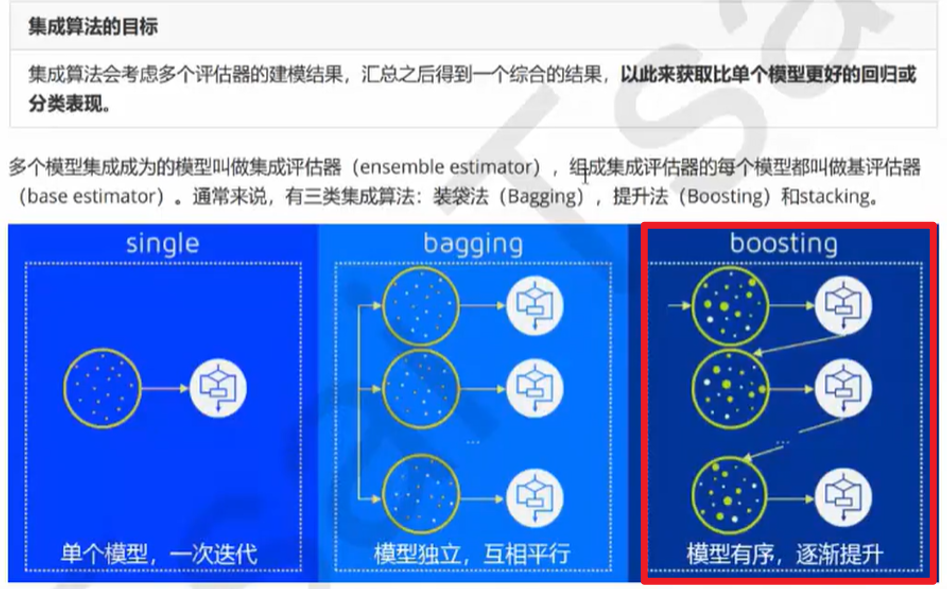
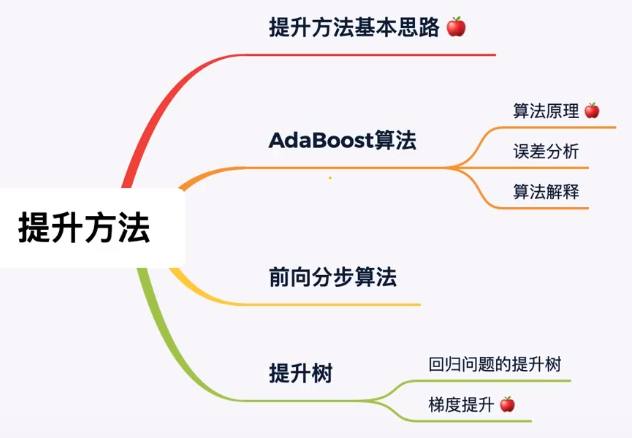
提升方法：将弱的可学习算法提升为强的可学习算法。其中提升方法是集成学习中的一种。

AdaBoost算法

准确的来说Adaboost是boosting的其中一种方法。采用了exponential loss function（其实就是用指数的权重）。
AdaBoost是提升法的一种，叫做梯度提升树。

改进：赋予权重。

那么都哪些东西需要权重呢？

答：相较于Bagging算法，Boosting算法根据整体数据上分类效果给予了不同臭皮匠不同的权重。根据单个数据上分类效果给予单个数据不同的权重。

为什么要赋予不同模型权重？

机器学习是一个前期通过不断学习、不断的改进，得到的一个遇到新的数据能够做出决策的机器。

举个例子：就好像一个学习去刷一套练习题一样，我们可以试想一下不同的臭皮匠就类似于一个班级上不同的学生，他们对同一套题目都进行了训练，经过验证最终A同学得了100分、B同学80分、C同学60分。我们认为A同学学习很好，C同学最差。现在又一场比赛需要三位同学应征出赛，在赛场上我们可以给予三位同学不同的权重。

我们给不同模型不同的权重可以使得学习的很好的臭皮匠在决策的时候起到更为重要的作用，而较差的臭皮匠起到弱的作用。误差大，分类器的权重低。（不需要傻子投票）

为什么要将单个数据赋予权重？

同样我们以同学参加考试为例，针对不同的题目，同学会有所感知，认为哪些题目很简单，so easy，而那些题目非常难。针对很简单的题目我们给予一个较弱的权重，针对一个很难的题目我们给予一个较大的权重，让后续的臭皮匠多多注意这些难的数据点。——有点像我们上学的时候的错题本，如果做过一个题很难，我们就多重视下这个题目。

算法流程

基分类器

在集成算法中，虽然大多都是通过树模型来实现的。但是也并不是说不能用逻辑回归等其他模型作为基分类器。下面Adaboost算法中，为了简单化，我们使用简单二分类器作为基分类器，做一个简单的Demo。在实际应用中，可以使用决策树、逻辑回归等等其他机器学习分类算法作为基分类器。

算法步骤

初始化/更新当前权值分布
训练当前基分类器
计算当前基分类器$G_{m}(x)$在训练集上的误差率
计算$G_{m}(x)$的系数
更新到新的模型中
判断是否可以退出循环

Ps：公式(8.2)中log的底数为e。即：$\alpha _{m} = \frac{1}{2} ln(\frac{1-e_{m}}{e_{m}})$

公式(8.3)和(8.4)可以改写成下面的形式：

$
w_{m+1,i} = \left\{\begin{matrix}
\frac{w_{mi}}{Z_{m}}e^{-\alpha _{m}}, G= y_{i}& \\
\frac{w_{mi}}{Z_{m}}e^{-\alpha _{m}}, G!=y_{i}&
\end{matrix}\right.
$

解释上面的公式：臭皮匠预测出来的标签与原标签相符则乘积为1，如果不相符则乘积为-1。

举个例子

现有训练数据表：

初始化当前权值分布

训练当前基分类器

这里我们使用最简单的二分类器为示例。在实际的应用中可以使用决策树、逻辑斯特回归等等基分类器。

即x大于2.5，这个二分类器认为是负例、小于2.5的认为是正例。

计算误差率

计算$G_{1}(x)$系数

$\alpha _{m} = \frac{1}{2} ln(\frac{1-e_{m}}{e_{m}})$

当$e_{m}$=0.3时候，对应的$\alpha _{m}$为图上x = 0.3处值对应的y轴坐标：

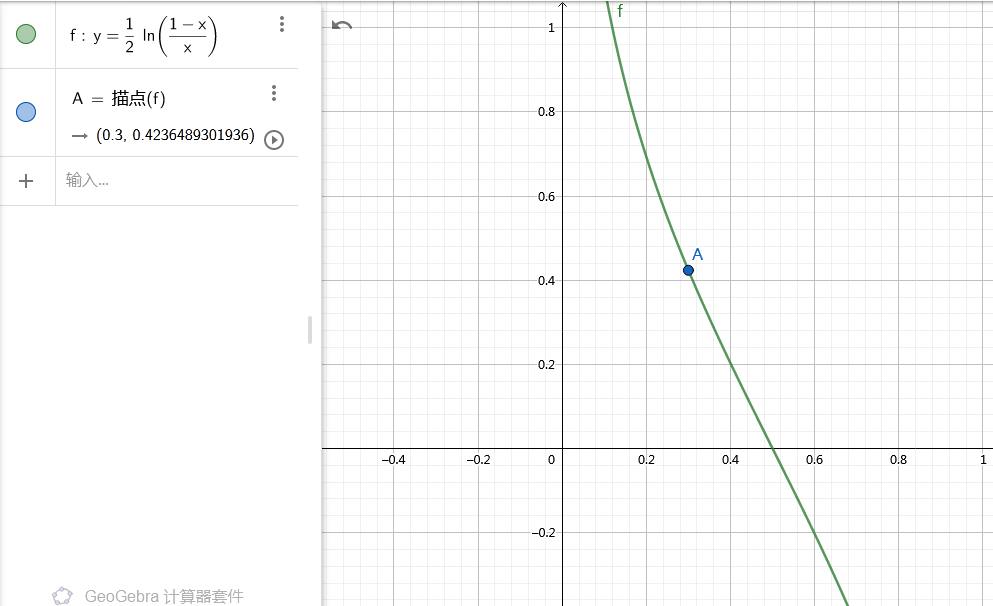
$G_{1}(x)$系数$\alpha _{m} = \frac{1}{2}ln(\frac{1-e_{m}}{e_{m}} ) = \frac{1}{2}ln(\frac{1-0.3}{0.3} ) = 0.4236$

更新权值到新的模型中

现在，m=1，根据公式(8.4) $w2i = \frac{w_{1i}}{Z_{1}} e^{-\alpha_{1}y_{i}G_{1}(x_{i}) },i=1,2,..,10$

Ps：Z是一个规范化因子，可以使10个权重统一到0-1范围内，同时使得他们相加等于1。

为了便于理解，我们先不进行规范化来计算10个臭皮匠的权值分布。

i从1至10，依此计算出下列结果：

$w_{21} = w_{11} e^{-\alpha_{1}y_{1}G_{1}(x_{2}) } = 0.1\times e^{-0.4236\times1\times1} =0.1\times0.65468570382251387556514129705002 \approx 0.0655$

$w_{22} = w_{12} e^{-\alpha_{1}y_{2}G_{1}(x_{2}) } = 0.1\times e^{-0.4236\times1\times1} =0.1\times0.65468570382251387556514129705002 \approx 0.0655$

$w_{23} = w_{13} e^{-\alpha_{1}y_{3}G_{1}(x_{3}) } = 0.1\times e^{-0.4236\times1\times1} =0.1\times0.65468570382251387556514129705002 \approx 0.0655$

$w_{24} = w_{14} e^{-\alpha_{1}y_{4}G_{1}(x_{4}) } = 0.1\times e^{-0.4236\times-1\times-1} =0.1\times0.65468570382251387556514129705002 \approx 0.0655$

$w_{25} = w_{15} e^{-\alpha_{1}y_{5}G_{1}(x_{5}) } = 0.1\times e^{-0.4236\times-1\times-1} =0.1\times0.65468570382251387556514129705002 \approx 0.0655$

$w_{26} = w_{16} e^{-\alpha_{1}y_{6}G_{1}(x_{6}) } = 0.1\times e^{-0.4236\times-1\times-1} =0.1\times0.65468570382251387556514129705002 \approx 0.0655$

$w_{27} = w_{17} e^{-\alpha_{1}y_{7}G_{1}(x_{7}) } = 0.1\times e^{-0.4236\times1\times-1}=0.1\times1.5274504913751733121398662471781\approx 0.1527$

$w_{28} = w_{18} e^{-\alpha_{1}y_{8}G_{1}(x_{8}) } = 0.1\times e^{-0.4236\times1\times-1} =0.1\times1.5274504913751733121398662471781\approx 0.1527$

$w_{29} = w_{19} e^{-\alpha_{1}y_{9}G_{1}(x_{9}) } = 0.1\times e^{-0.4236\times1\times-1} =0.1\times1.5274504913751733121398662471781\approx 0.1527$

$w_{210} = w_{110} e^{-\alpha_{1}y_{10}G_{1}(x_{10}) } = 0.1\times e^{-0.4236\times-1\times-1} =0.1\times0.65468570382251387556514129705002 \approx 0.0655$

现在计算出了权值分布，下一步是将其规范化。

为什么要规范化？

如何规范化？

计算规范化因子，见公式(8.5)。

$Z_{1} = \sum_{i=1}^{N} w_{1i}e^{(-\alpha _{1}y_{i}G_{1}(x))} $

$= 0.1\times e^{(-0.4236\times1\times1)}+1\times e^{(-0.4236\times1\times1)}+…+1\times e^{(-0.4236\times-1\times-1)} $

$= w_{21}+w_{22}+…+w_{210}$

$= 0.0655+-0.0655+…+-0.0655$

$= 0.9166$

Ps：其实就是将上面我们计算出的$w_{21}$~$w_{210}$相加后得到的。

然后再上面的每个$w_{21}$~$w_{210}$各自除以$Z_{1}$得到规范化后的值：

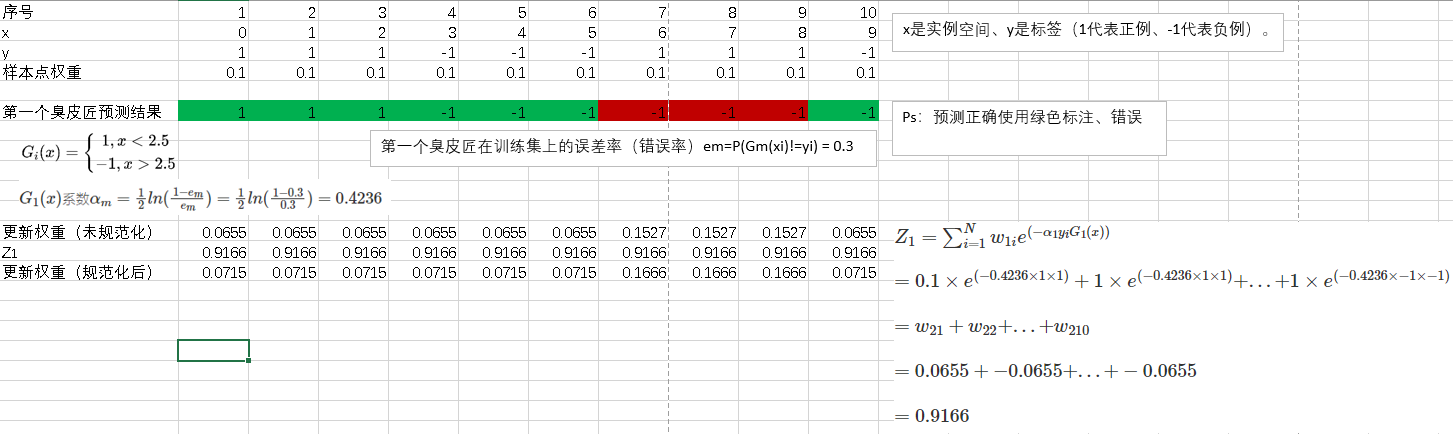
接下来另m=2、m=3 … 循环计算。直到遇到终止条件。

终止条件

可以从分类器是否达到个数作为终止条件。
总分类器误差率是否达到设定精度。
误分类点个数达到设定条件（例如要求误分类点个数为0）。

最终得到的分类器为：

图解

参考文献：

《统计学习方法》李航

https://www.bilibili.com/video/BV1x44y1r7Zc?p=3

https://www.bilibili.com/video/BV1i4411G7Xv?p=8

作者：高志远

高志远，24岁，男生查看高志远的所有文章

集成方法之Boosting提升方法：更像现实中实际学习的模型