本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
从神经细胞提出感知器模型

左图神经元(神经细胞)树突接受电信号,我们认为电信号只有高低,那么它自然可以用数字来表示(即 X1~Xm)。经过处理后由突触输出电信号,这里的处理可以理解为树突对电信号的加工,我们用数学模型模拟的是乘积。树突是有权重的,用wk1~wkm来表示。乘完之后对其求和,这里的求和模拟的是神经元的运动。随后加上一个偏置,这种偏置描述的不同神经元所处生理环境的不同。最后得到一个输出,还有一个激活函数对这个值进行最后的改造。
你可能觉得这很玄学,没错!就是这样,这毫无根据,生命十分深奥,虽然神经元是生物神经系统传递信息和感知的结构,但生物体内的神经元与深度学习中的神经网络并没有什么直接关系,也就是说并不是代码实现了生物体的神经元结构,直到今天为止,现代医学对生物体神经元的研究也没有很确切。
前沿:
- 目前也有一些人想从生物学得到启发,试图有人用采集神经细胞,然后用电刺激神经元试探出神经元处理后的结果。
- 有人试图创建新的数学模型去模拟生物体内的不同神经细胞。

1957年,Frank Rosenblatt本身是计算机出身的,它看到了上面的数学模型后,将其整理为算法。
感知机模型是


在我们之前提出划分红豆绿豆问题时就涉及到了感知机的思想,可以再回顾下: 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
使用增广向量简化编程算法

使用增广向量的目的就是让计算变得更加简单,变成了找w问题。
感知器算法的收敛证明与代码实现
关于感知机模型的推导、证明、代码实现都可以参考上面的文章。这里不再过多赘述。
这部分可在视频第20讲第21分观看!也可以参考书«统计学习方法»。
人工智能的第一次寒冬:日常中的很多问题是非线性可分的
因为日常中的很多问题是非线性可分的,所以要引入非线性函数。
地位不可分,但是升高纬度可能就可划分,老师举了一个反例说明了现实中的很多问题都是非线性可分的,这一部分不是很懂,稍后再看。
解决非线性可分:引入多层神经网络
分开函数的集合也要变成非线性的,这样才使得用人工智能解决现实中的非线性问题成为可能的道路。
也就是说,因为现实中的大多数问题非线性可分,所以神经网络应该是可以划分非线性的问题才行!不然就基本没用!
包含两层神经网络,两层中间的$\varphi $是一个非线性函数。

如果不加$\varphi $则是线性函数

可以将其一笔写出:
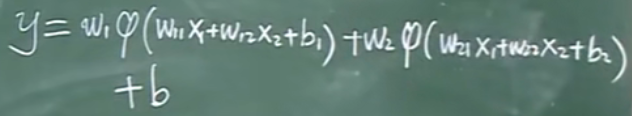
如果没有$\varphi $,就跟一个单一的神经元模型一样了。
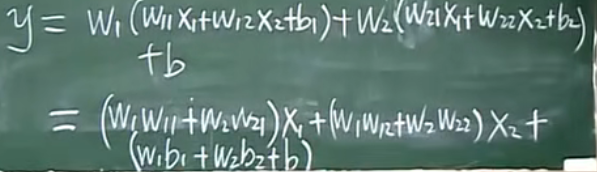
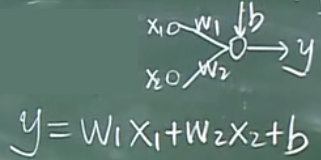
所以,只有加了非线性函数$\varphi $之后,才能让这个模型是非线性的。
问:引入的非线性函数$\varphi $是什么?
答:阶跃函数

有人证明过,如果使用阶跃函数可以解决所有的非线性模型。(具体证明可自行查找)
三层神经网络可以模拟所有决策面
用神经网络模拟决策面:
下图一个平面有C1和C2两种分类结果,也就是两种决策面。
我们需要构造一个函数,落入C1的点(x1, x2)的函数值>0,如果落在C2则函数值<0。
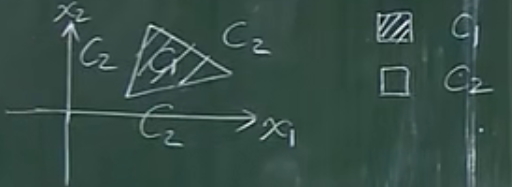
合理的构造决策面使w1、w1、w3都为1,y>0。否则y<0。

如何去做?
很简单,使w都等于1,b取-2.5。这样只有三个都是1,加起来是3,减去2.5得到的y是大于0的;如果只有两个1,加起来减去2.5<0。满足条件。

现在我们用两层神经网络模拟了三角形决策面,接着推:
决策面是四边形:

以此类推,如果是五边形,就增加神经元个数。
如果是圆形就有无限多个神经元,是我们熟知的微元法:

如果是出了圆以外的其他情况:

三层神经网络可以模拟任意决策面:
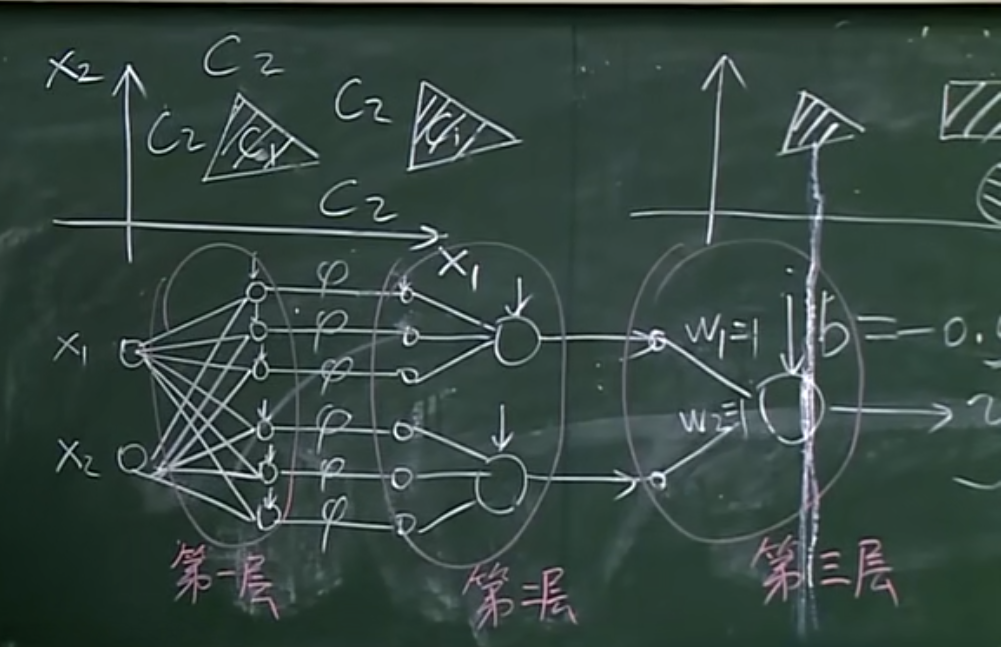
第一层判断是否在直线一侧,第二层判断是否在特定区域内,第三层判断是否在区域内(有点像数字电路的与或逻辑关系)。
后向传播算法(bp算法)
每一层可以设计不同神经元的个数,也可以设计层的个数。那么对一个具体的问题如何设计合理的层数以及神经元个数?
答:到目前为止理论方面并不完善,我们还是只能通过实验的方式来确定层数以及神经元的个数,是通过经验来获得的。
下面我们要讲的算法就是bp算法—后向传播算法。bp算法的主要思想是梯度下降法求局部极值。
常用的非线性函数(激活函数)
这是我们最常采用的两个非线性函数:


为什么要使用这些非线性函数?因为他们的导函数都很简单。没错,就是因为简单我们才用。
下面再讲两个在深度学习出来之后出现的两个非线性函数:
ReLU


Ps:有错误,不连续不可导。
为什么引入ReLU函数?
答:ReLu会使一部分神经元的输出为0,可以使得神经元消失,不发挥作用,造成了 网络的稀疏性,并且减少了参数的相互依存关系,避免过拟合的发生。
LeakReLU
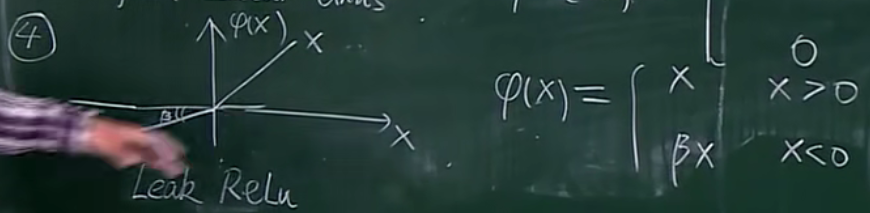
BP算法中核心的数学工具就是微积分的链式求导法则。
为什么要用链式求导法则?


告诉我们1个单位的b变化会引起1个单位的c变换,
告诉我们 1 个单位的c变化会引起2个单位的e变化。
例如通过e = c*d求出a的值,就是计算e对a求偏导。根据链式求导法则,需要计算:
$\frac{\partial e}{\partial a} = \frac{\partial e}{\partial c} * \frac{\partial c}{\partial a}$
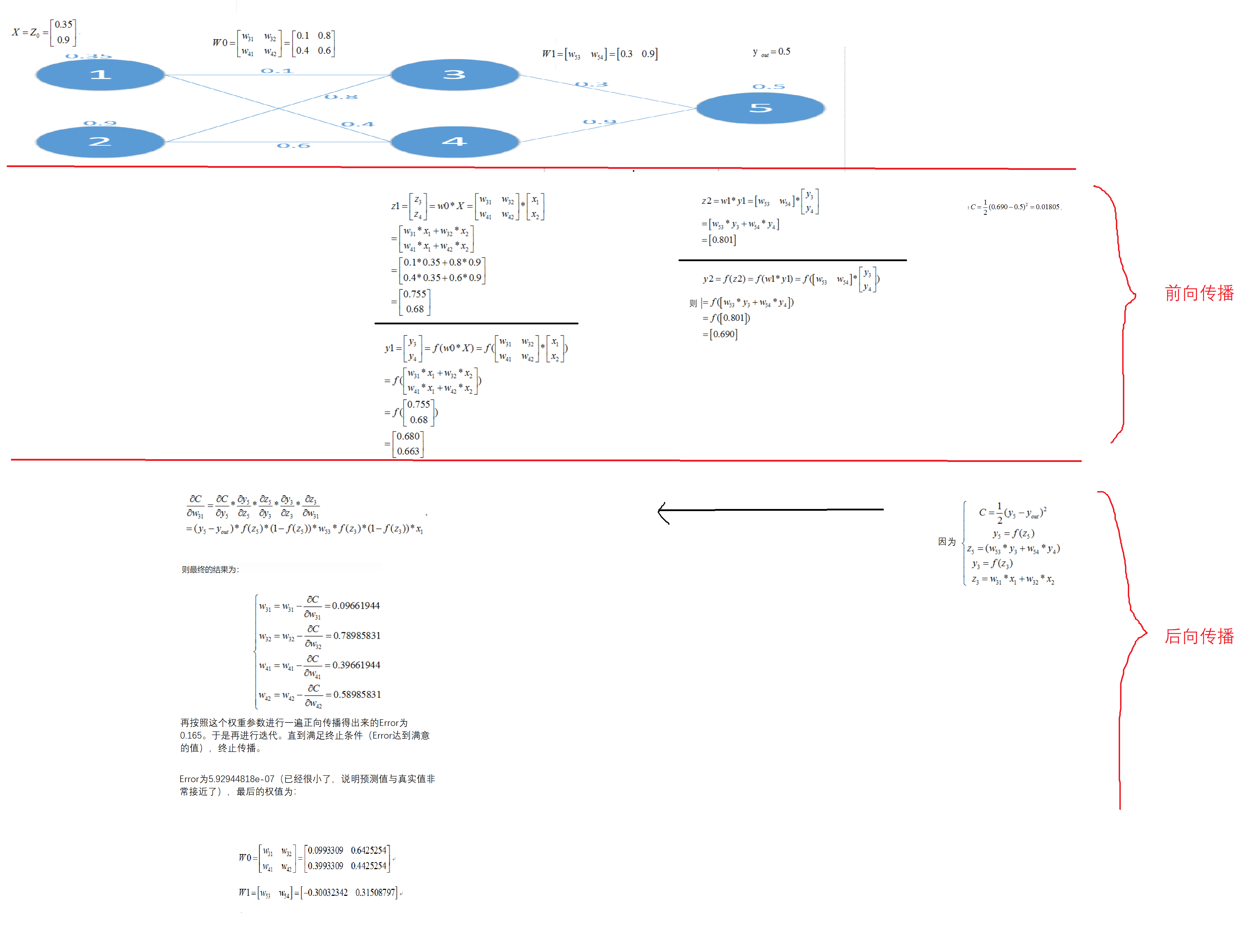
前向传播&后向传播算法
前向传播可以计算出Error。
反向传输(BP)算法即用来高效的计算这些参数的偏导数,进而得出成本函数(损失函数L)的梯度。
bp算法参数

在训练集上目标函数的平均值(cost):
- 理论上训练出来的cos的值应该是逐渐减小的,他减小到一个程度我们可以设定一个阈值,到这个程度上终止继续的迭代。
- 如果函数的下降在某一刻突然的增加,那我们就要及时的终止他,因为有可能是神经元的个数不够导致训练出来的模型不能够捕获到我们训练集上所有的特征,也就是说该模型不够强大,要对模型进行改进。
停止准则:
我们一般不以这个cost的值来作为我们的终止准则,因为这个cos的值是逐渐的趋向于零,但他不会等于零,如果我们不加以限制的让这个cost的值训练的很小很小,那么就会出现过拟合的问题。通俗的来说,就是矫枉过正,这个模型它会在我们的训练集上表现的非常优秀,但是无法在一个新的数据集(验证集)上面得到一个良好的效果。所以训练一段时间之后,必须要在编程题上面去测试。这就好像是一个考试一样,我们在学习的阶段。通过训练的方式来不断的锻炼自己,但是我们不能无限制的这样去锻炼,我们需要一个验证考试去来评判我们的模型在真实环境下(考试中)是否可以良好地进行表现。也就是说,平时的学习不要矫枉过正,目的是为了将来的考试,要保存验证集上最好的结果作为训练模型。
学习率:
如果学习率比较大就会导致模型不好收敛。如果学习率比较小就会导致模型的训练时间过长。
参数设置


这一部分可以参考,随机梯度下降和全批量梯度下降,之前的略涉及到,逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
神经网络优势

劣势

针对第三点,在小样本(一般是小于5000)使用svm就可以达到比较好的效果。针对大量样本,神经网络具有优势。
人工神经网络近期趋势
- 卷积神经网络(用于图像数据)
- 递归神经网络(用于序列数据,例如时间序列或者空间序列)

- 无监督模型:自动编码器
- 生成模型:生成性对抗网络
参考文献:
https://www.bilibili.com/video/BV1dJ411B7gh
https://zhuanlan.zhihu.com/p/24801814
https://blog.csdn.net/weixin_44538273/article/details/86677644