多元函数的梯度上升我们可能不好理解,二元函数的梯度函数是一个曲面,我们现在用最简单的一个一元二次函数:
$f(x) = -x^2+3x+1$
函数图像:
使用高中方法计算最大值
先对原函数求导:$f(x)’ = -2x+3$,另 -2x+3=0,解出x = 1.5。即在x=1.5处取得极大值。
使用梯度上升法计算极大值
在机器学习中,各种多元函数层出不穷。花样各异。并不会像上面这道题这么简单。往往是求出导数后也很难精确计算出函数的极值。
依靠程序的特性(穷举),一步步去做,逐步试错,最终得到极值点。
使用穷举迭代的方法来做。就像爬坡一样,一点一点逼近极值。这种寻找最佳拟合参数的方法,就是最优化算法。爬坡这个动作用数学公式表达即为:
$x_{i+1} = x_{i}+\alpha \frac{\partial f(x_{i}) }{x_{i}} $
其中,α为步长,也就是学习速率,控制更新的幅度; $\frac{\partial f(x_{i}) }{x_{i}} $代表$f(x_{i})$对$x_{i}$求偏导。
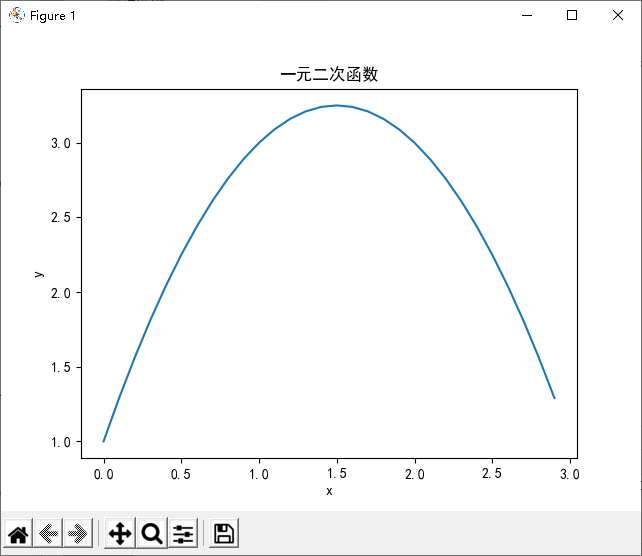
从x = 0位置开始迭代,学习步长alpha = 0.00001。精度presision = 0.000000001。经过若干次迭代后即可逼近我们要的极值点。这一过程,就是梯度上升法。
import numpy as np
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
def Gradient_Ascent_test():
x_old = -1 # 初始x位置值
x_new = 0 # 开始梯度上升的x的初始值
alpha = 0.00001 # 学习速率(步长)
presision = 0.000000001 # 精度,用于截止
while (x_new - x_old) > presision:
x_old = x_new # 赋新的x
x_new = x_old + alpha * (-2 * x_old + 4) # 迭代的下一次x位置
print(x_new)
def draw():
# 一元二次函数图像 参考:https://blog.csdn.net/manchan4869/article/details/117295396
x = np.arange(-5, 10, 0.1)
y = -x * x + 4 * x
plt.xlabel('x')
plt.ylabel('y')
plt.title("一元二次函数")
plt.plot(x, y)
plt.show()
if __name__ == '__main__':
draw()
Gradient_Ascent_test()