协方差
用途:衡量两个或两个以上数据间的独立性、相关性。
结论:
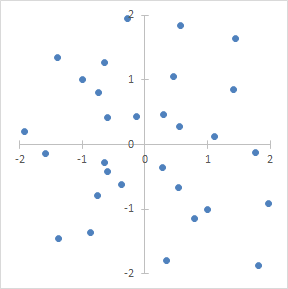
如果x和y的联合分布多分布在一三象限,x ⋅ y多为正数,则协方差为正,x和y正相关。
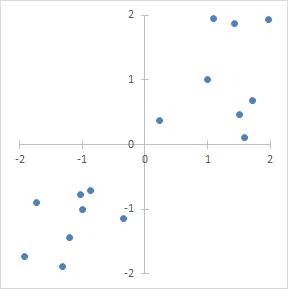
如果x和y的联合分布多分布在二四象限,x ⋅ y 多为负数,则协方差为负,x和y负相关。

如果x和y的几乎均匀地分散在所有象限中,则x ⋅ y 有正有负,均值接近于0,说明x和y之间没有相关性(只是说没有线性相关)。
协方差与方差
协方差本质就是不同维度数据间衡量其相关性,例如x与y之间数据相关性。
如果是x与x本身,都在同一纬度衡量相关性,这就是方差。
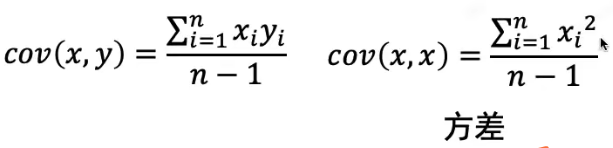
所以方差是特殊的协方差。
协方差矩阵
明白了协方差,协方差矩阵很好理解,其实就是2个或两个以上的维度交织在一起产生的多种相关关系,用矩阵的方式记录下来而已。他们数值之间的意义与协方差相同。

观察下面动图:
- 沿着x轴拉伸只改变协方差矩阵中左上角的cov(x, x)。相当于忽略掉y轴后,x轴自身数据变得离散或聚集,体现出的就是x自身的方差。
- 如果旋转,则改变了协方差矩阵中的所有协方差,因为x和y两个维度交织在一起产生的x与x、x与y,y与y之间相关关系均发生了改变。
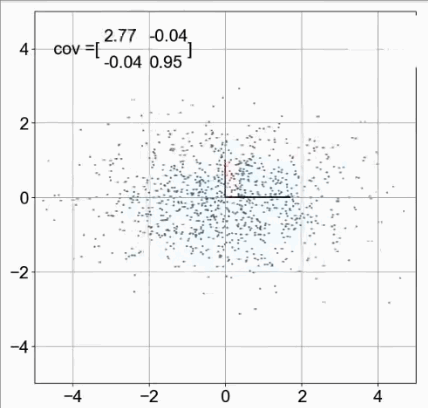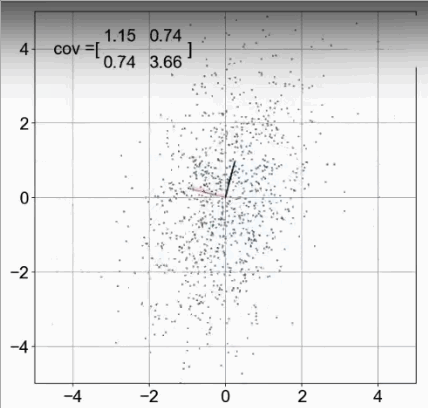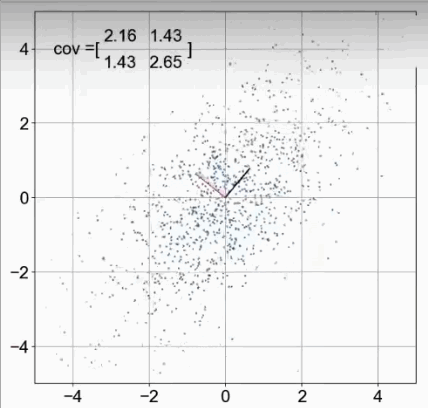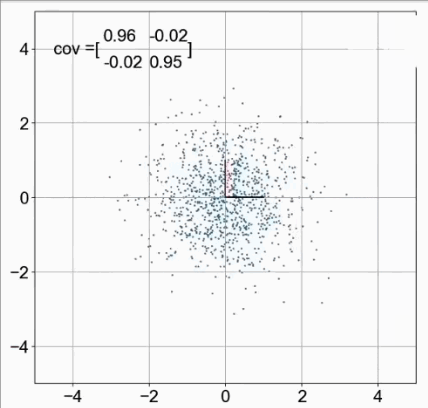
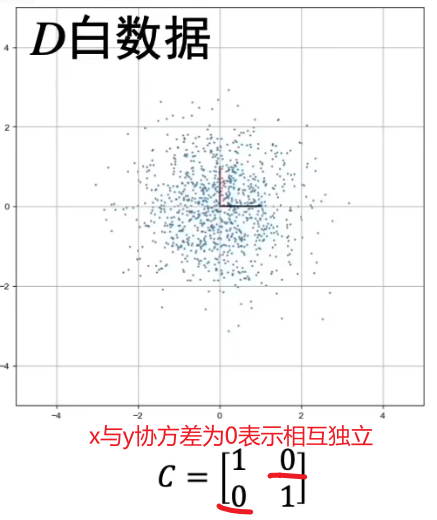
下图,x与x、y与y自身的协方差都是1。——这个我们暂时不研究。
但是,x与y之间的协方差为0,表示两者之间相互独立。
x与y的协方差>0,表示正相关。<0表示负相关。
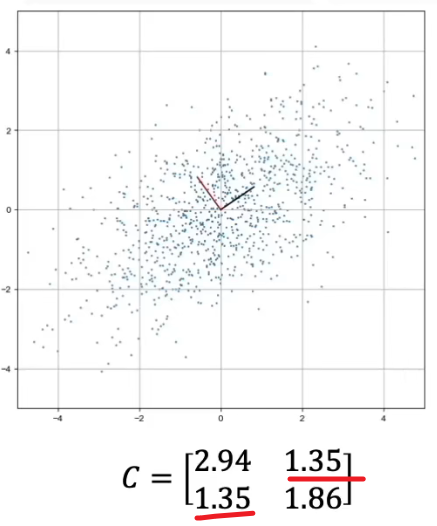
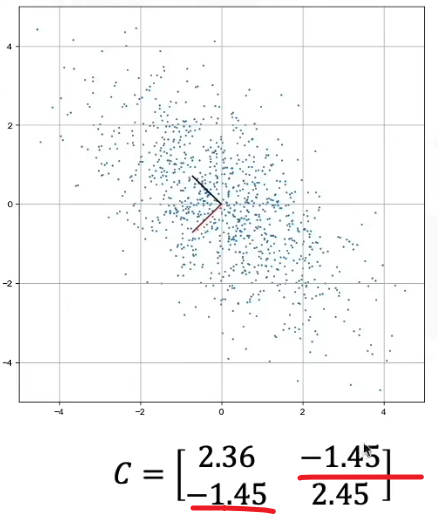
相关系数
为了克服协方差的缺陷而诞生的,
任何两个数变量的相关系数,必然是一个 -1 到 1 之间的值(证明略)。
相关系数为 1 ,说明两个变量完美正相关;
相关系数为-1 ,说明两个变量完美负相关;
相关系数为 0 ,说明两个变量完美不相关。
转载自:
https://blog.csdn.net/hustqb/article/details/90264432