本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
书接上文:回忆感知机红豆绿豆模型
之前我们学习过感知机的概念和应用,回忆:感知机 – 一种二分类线性分类模型,划分红豆和绿豆
我们解决了一个分类问题——划分红豆和绿豆。我们可以让机器随心所欲的正确划分出一条直线将图中的红豆和绿豆划分开。
现在我们有了一个更好的划分红豆和绿豆的模型,它可以找出最合适的划分线。
我们想找到一个最好的、最优的超平面
回想我们之前的感知机模型,虽然可以找到一个超平面,但是这个超平面并不一定是最优的。
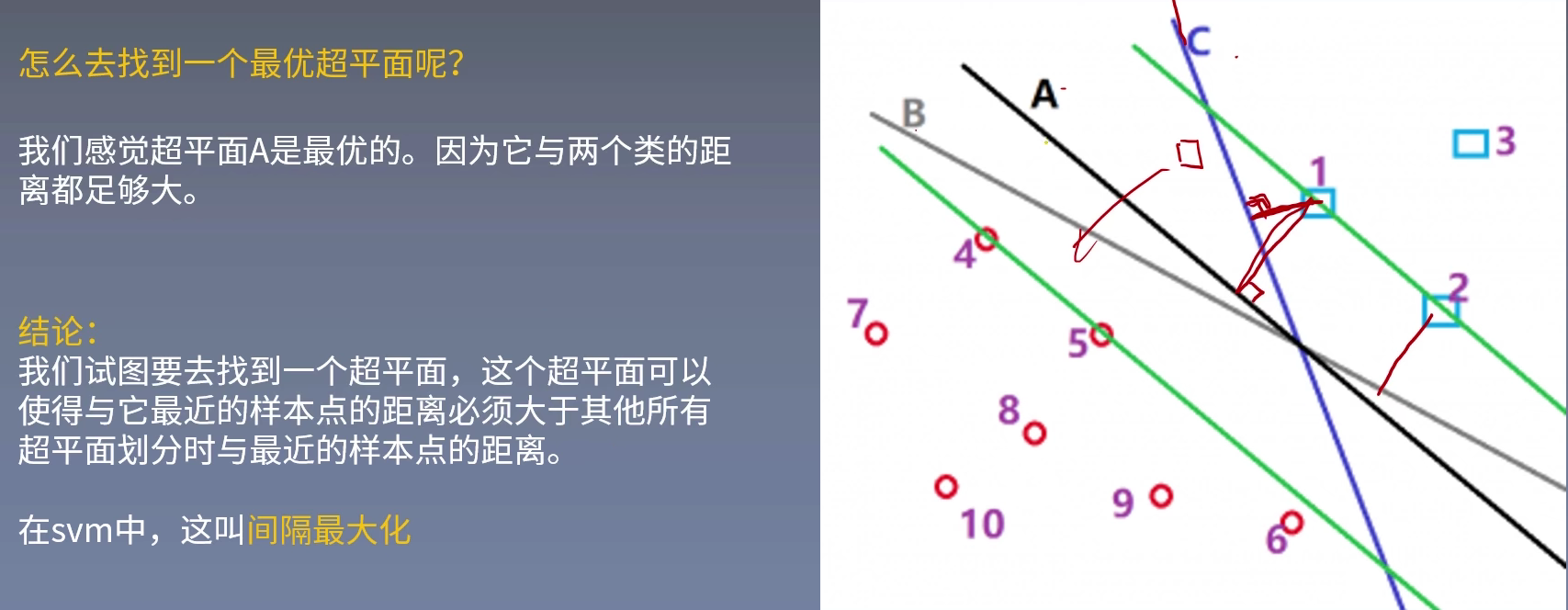
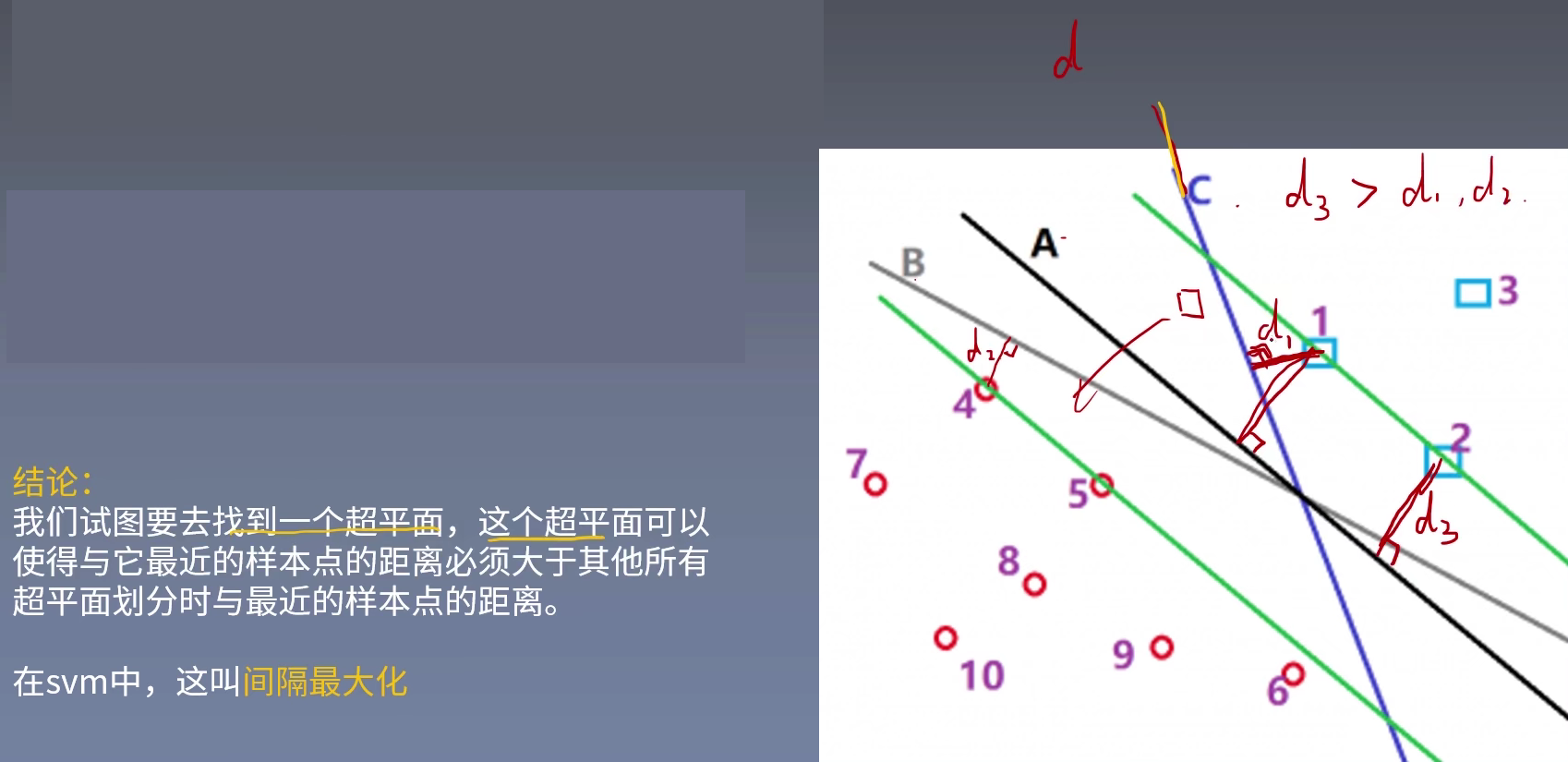
例如下图,在感知机中,找到的超平面根据起始位置、红豆绿豆点位置处理顺序不同,得到的超平面会有很多种,例如线A、B与C。
我们先直观的认为,线A要比线B和线C要好得多。
低维不可分



支持向量积解决什么问题?——答:支持向量积最本源就是一个线性分类器。分类,不光要分的开,而且想要分的更好。
怎样才能分的好呢?——答:分的开,分的远。
支持向量机分类

函数间隔和几何间隔
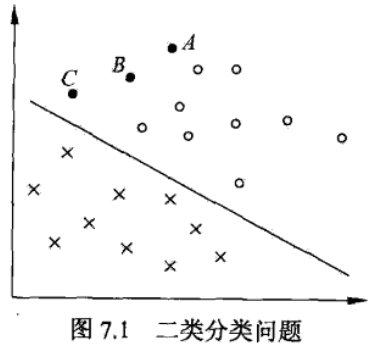
在上图中点代表正例,叉代表负例。A、B、C是三个实例点。超平面为$w^Tx+b=0$,$|w^Tx+b|$代表实例点与超平面的远近,在一定程度上可以表示分类预测的可信程度。
其中,$y_{i}$表示实例点的标签,有+1(正例)和-1(负例)两个值,$w^Tx+b$与y的符号可以表示当前分类是否正确。
综上所述得到下图的函数间隔公式:
$\hat{\gamma } = y_{i}(w^Tx+b)$
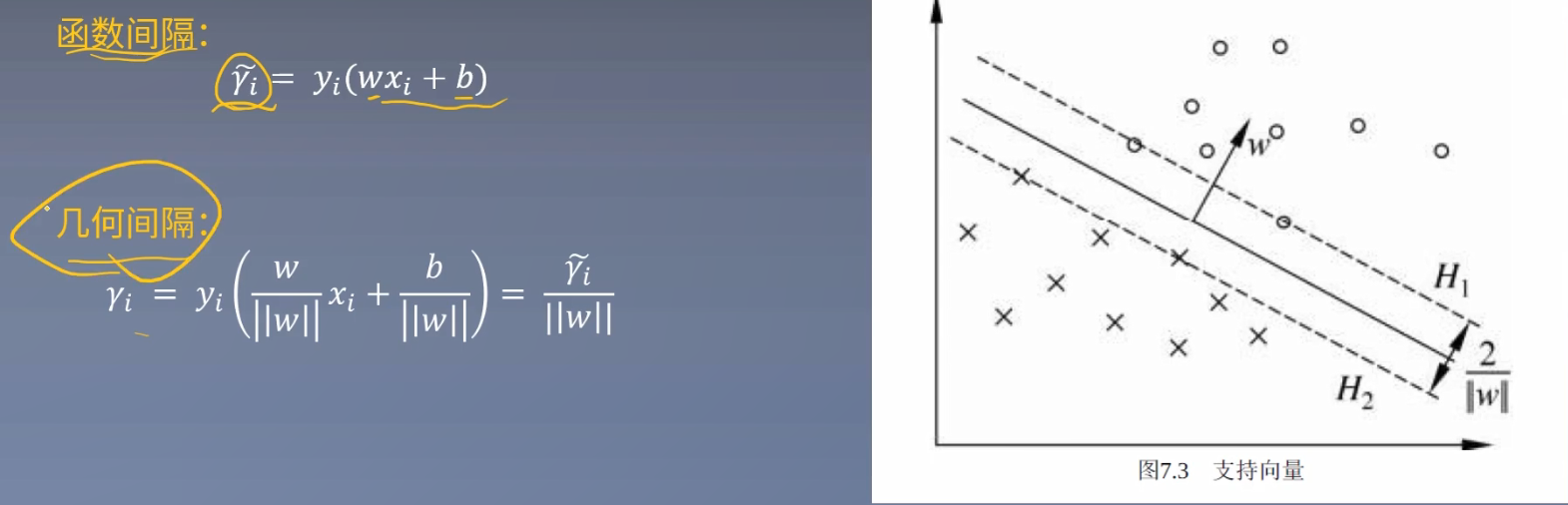
但我们并不使用函数间隔,接下来需要对w和b做规范化处理,使其间隔成为确定的,不受w和b成比例缩放的影响。——这一点在感知机章节已经介绍过了。
为什么不使用函数距离而使用几何距离?
https://www.bilibili.com/video/BV1g64y1h7Lc?p=17

从图上来看,同样的距离,用函数距离会得到不同的结果。
如果用函数距离衡量点到不同超平面的距离,就会出现上述例子里出现的问题。所以,一个点到不同超平面的距离不能用函数距离来表示。
但函数距离也是有意义的,如果给定一个超平面,衡量不同的点到超平面的距离。可以用函数距离来表示。

由此可推出在高维情况下向量(一阶矩阵)到超平面的几何距离为:

上面的d公式即为几何间隔。
间隔最大化
回想感知机,虽然能正确划分数据,但是得到的超平面有许多个,并不是唯一的。在支持向量机中,我们想要得到是一个前提正确的、并且拥有充分大的可信度划分出来的唯一一个最优超平面。
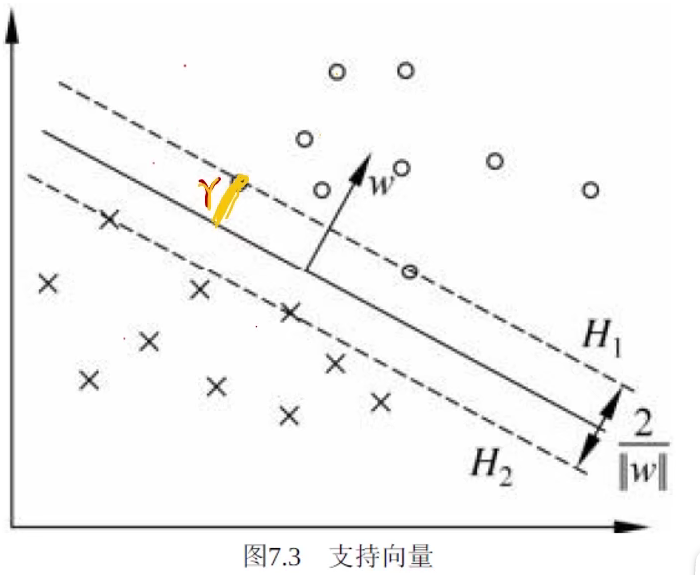
定义最近的点离超平面的距离是$\gamma$我们想最大化上面的这个$\gamma$。
其他所有的样本点都要大于这个$\gamma$,即:

如果样本点在上面,它与与超平面的距离是正数,乘以label,得到正数。
如果是下面的样本点,距离是负数,乘以label负数,得到的也是正数。
用函数间隔得到等价最优化问题
因为w和$y_{i}$并没有什么关系,所以可以将w提前,然后拆分成两个子问题。
且函数间隔与几何间隔存在转换关系式,所以可将问题改写为下面的情形:

$\gamma $的取值不影响最优化的解
我们如果将w和b的值等比例的缩放2倍,那么就变为$y_{i}(2w^Tx+2b)\ge 2\hat{\gamma } $,此时函数间隔变为$2\hat{\gamma } $。
上面的$max\frac{\gamma }{\left | \left | w \right | \right | } $变为$max\frac{2\gamma }{\left | \left | 2w \right | \right | } $化简后并不影响上述最大值和不等式。
既然这样,我们就可以取$\gamma$=1,得到:

为什么分子取1?

a的作用就是将最适合的那个超平面移到中间的位置。
最大化转为最小化问题
求w的二范数和求w的二范数的平方在其他方面可能不等价,但是在求最小值方面一定是等价的。
并且,$max\frac{1}{\left | \left | w \right | \right | } $等价于$min\left | \left | w \right | \right | $。因为上面说过$\gamma $的取值不影响最优化的解。所以我们为他乘以1/2常量。
所以![]() 。
。
于是得到下面的线性可分支持向量机学习的最优化问题:
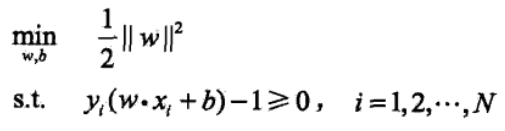
为什么前面加了个1/2?
为了后面的求导方便。
现在就是凸二次规划问题了。
拉格朗日乘子法
$L(w, b, \alpha ) = \frac{1}{2}||w|| ^2-\sum_{i=1}^{N}\alpha _{i}[y_{i}(w^Tx_{i}+b)+1] $
$=\frac{1}{2}||w|| ^2-\sum_{i=1}^{N}\alpha _{i}[y_{i}(w^Tx_{i}+b)]+\sum_{i=1}^{N}\alpha _{i}$
其中不要忘记我们上面的约束条件是一直存在的。
对偶问题
KKT条件为我们证明出来的对偶性质,它可以帮助我们推导。(我们暂时不用去看KTT推导,暂时认为是对的就可以了,知道就可以了!)
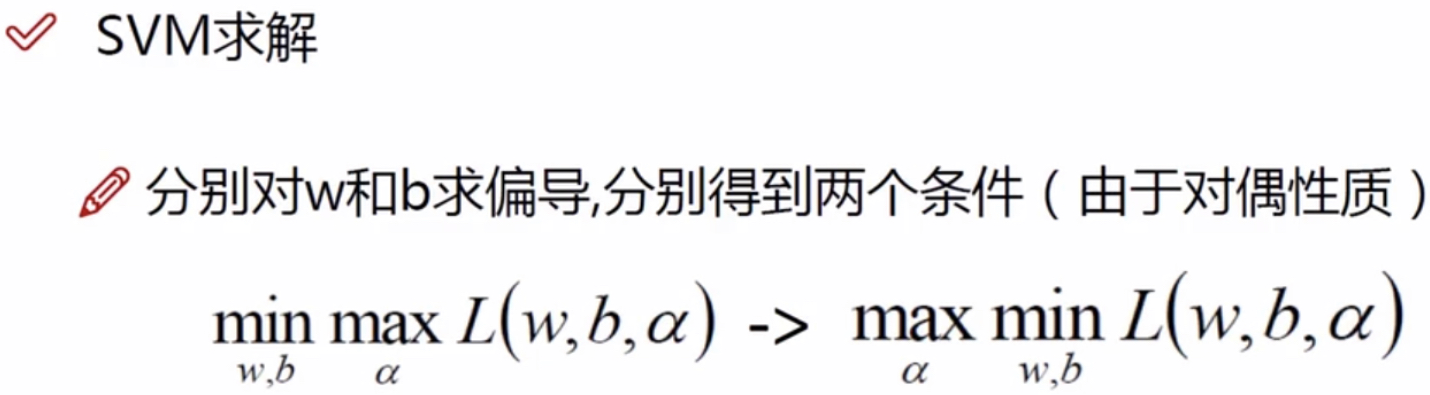
需要对w和b求导:
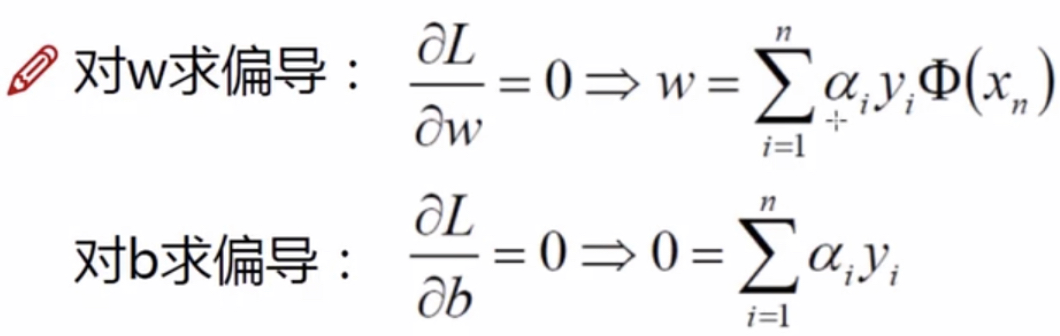
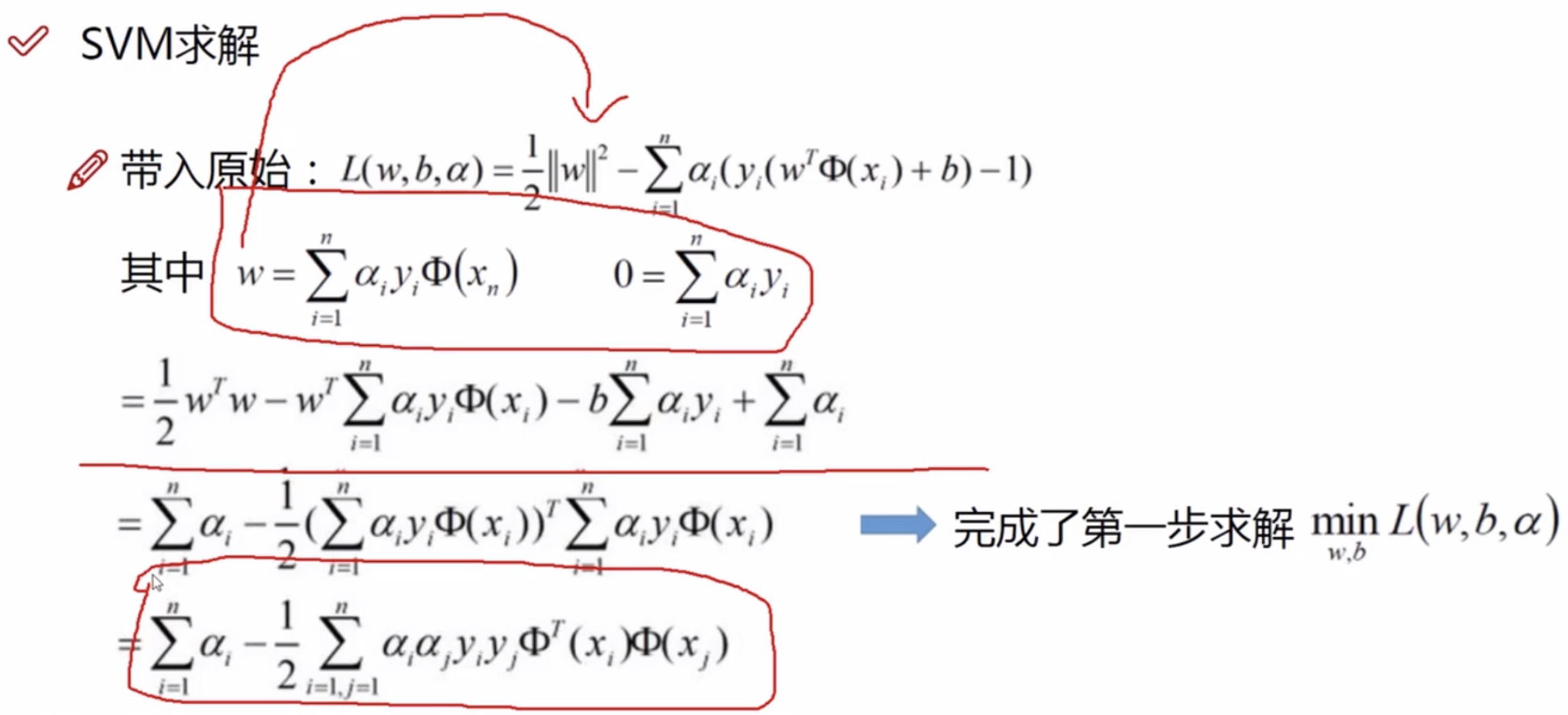
将w和b带入原始L函数:
支持向量机求解实例
支撑向量


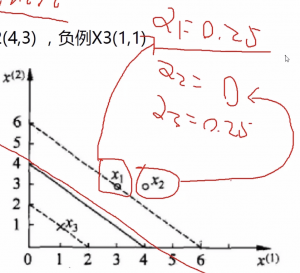
数据代入可参考下图,其中$\alpha _{i}$,i可取1、2、3。


因为,$\alpha _{1}+\alpha _{2}=\alpha _{3},所以\alpha _{3}=0.25$
哪些点是起作用的点
例子中的三个点,只有在虚线上X1、X3的两个点的$\alpha _{1}$和$\alpha _{3}$非0,他们对应的w的值也不为0。相反,不再虚线上面的点x2,它的w值一定为零。这也就解释了支持向量机的本质是支撑向量,对其有影响的点才会起到支撑作用,改变w的值。这里的点x1和x3叫做支持向量。
参考文献:
https://www.bilibili.com/video/BV1i4411G7Xv?p=7
https://www.zhihu.com/question/38586401
https://www.zhihu.com/collection/740229096
https://b23.tv/BV1UR4y147AT/p8