本文已收录到:机器学习笔记 专题
- 机器学习的学习顺序、书籍和一些体会
- 朴素贝叶斯 – 根据男性特征分析女性是否嫁的问题
- 感知机 – 一种二分类线性分类模型,划分红豆和绿豆
- 逻辑斯谛回归 – 不那么生硬的划分红豆和绿豆
- 支持向量机:线性可分支持向量机与硬间隔最大化
- 支持向量机:线性可分支持向量机与软间隔最大化
- 利用集成方法提高基分类器分类性能
- 集成方法之Bagging装袋法:三个臭皮匠投票、少数服从多数
- 集成方法之Boosting提升方法:更像现实中实际学习的模型
- 决策树不仅可以做分类,还可以回归:回归树
- K-均值聚类算法,对无标签数据进行分组汇聚
- Apriori算法进行关联分析
- 使用FP-growth算法高效的挖掘海量数据中的频繁项集
- 维度是什么?数据降维方法,降维的用途
- 最广泛的降维算法:主成分分析(PCA)【原理讲解+代码】
- 人工神经网络(ANN)及BP算法原理
- 深度学习常用数据集、发展脉络和工具框架介绍
- 自编码器 – 经典的无监督学习神经网络、领会它的思想
- 卷积神经网络:卷积就是特征提取器,就是CBAPD
- 循环神经网络(RecurrentNN):有记忆的神经网络
解决什么样的问题?
朴素贝叶斯算法是有监督的学习算法,解决的是分类问题,如客户是否流失、是否值得投资、信用等级评定等多分类问题。
什么是有监督学习?无监督学习?
有监督学习:有标签
无监督学习:聚类” (clustering),聚类目的在于把相似的东西聚在一起
可以解决的典型问题
一句话总结,就是基于特征做二元决策。
- 垃圾邮件分类(是否为垃圾邮件)
- 客户是否流失、是否值得投资、信用等级评定等
例题 – 根据男性特征分析女性是否嫁的问题
下面我先给出例子问题。
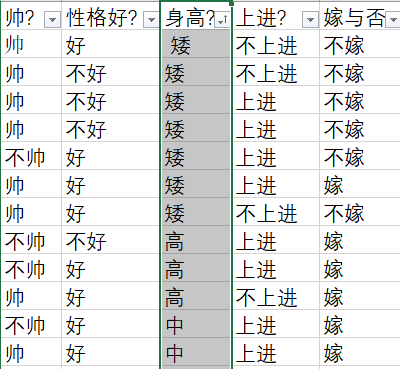
给定数据如下:该数据共计有四个字段和一个标签。
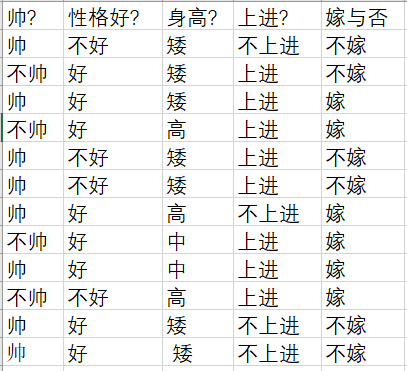
现在给我们的问题是,新来一个男生,他有以上四个特征,分别是:不帅、性格不好、身高矮、不上进,我们来机器判断是否嫁。
这是一个典型的分类问题,最后我们期望得到的结果要么是嫁、要么是不嫁。
转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,就给出相应的答案。
根据贝叶斯公式,左侧的公式是我们期望计算出来的结果值,右边是通过贝叶斯公式得出的需要计算的公式。
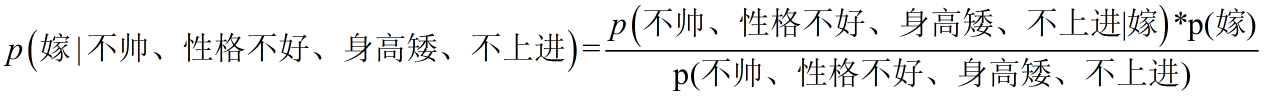
为什么需要假设特征之间相互独立呢?
但是为什么需要假设特征之间相互独立呢?
1、我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*3*3*2=36个。
24个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
2、假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),
我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
我们将上面公式整理一下如下:

等式成立的条件需要特征之间相互独立,朴素贝叶斯算法是就是假设各个特征之间相互独立的。
* p(不帅、性格不好、身高矮、不上进) 下面我将一个一个的进行统计计算(在数据量很大的时候,根据中心极限定理,频率是等于概率的,这里只是一个例子,所以我就进行统计即可)。
p(不帅、性格不好、身高矮、不上进|嫁)
p(不帅、性格不好、身高矮、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁)。
P(A|B)——即事件A 在另外一个事件B已经发生条件下的发生概率。
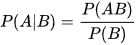
根据最开始给出的表,共计有12个样本,可以分别计算出上面的四个值:

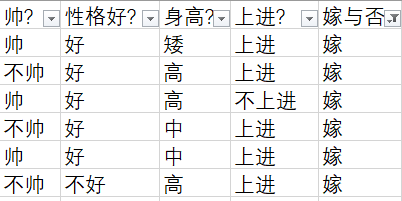
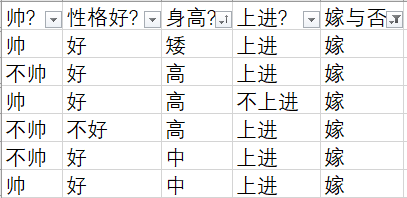
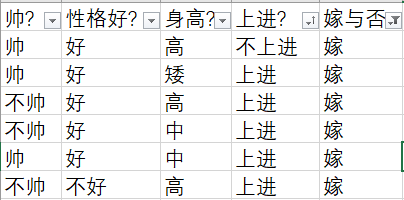
- p(不帅|嫁) = 3/6
- p(性格不好|嫁) = 1/6
- p(身高矮|嫁) = 1/6
- p(不上进|嫁) = 1/6
p(不帅、性格不好、身高矮、不上进)
p(不帅、性格不好、身高矮、不上进) = p(不帅) * p(性格不好) * p(身高矮) * p(不上进)
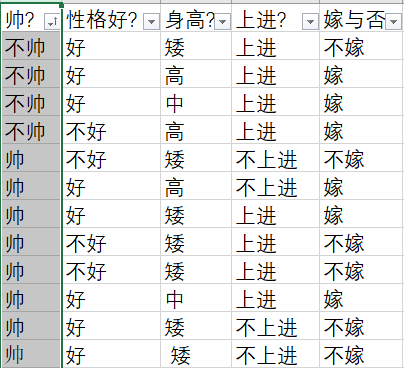
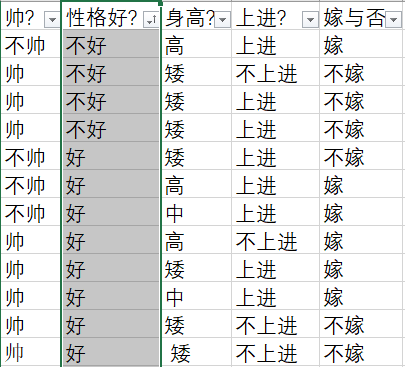
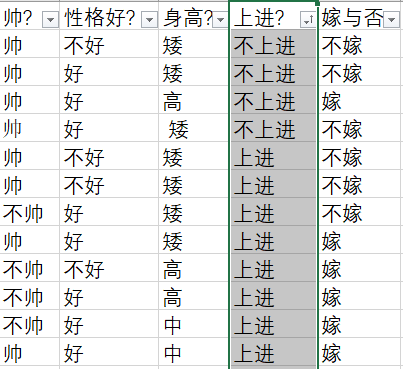
- p(不帅) = 4/12
- p(性格不好) = 4/12
- p/(身高矮) = 7/12
- p(不上进) = 4/12
p(嫁|(不帅、性格不好、身高矮、不上进))

得出结果,p(嫁|(不帅、性格不好、身高矮、不上进)) = (3/6 * 1/6 * 1/6 * 1/6 * 6/12)/(4/12 * 4/12 * 7/12 * 4/12) = 0.0535714286
同理可得,p(不嫁|(不帅、性格不好、身高矮、不上进)) = (1/6 * 3/6 * 1 * 3/6 *6/12)/(4/12 * 4/12 * 7/12 * 4/12) = 0.964285714
0.964285714 >> 0.0535714286。显然,我们的模型给出的结论是不嫁。
参考文献:
https://zhuanlan.zhihu.com/p/26262151
https://cuijiahua.com/blog/2017/11/ml_4_bayes_1.html
【数据仓库 数据挖掘 – 决策树分类 朴素贝叶斯分类算法-哔哩哔哩】https://b23.tv/u1xIpn