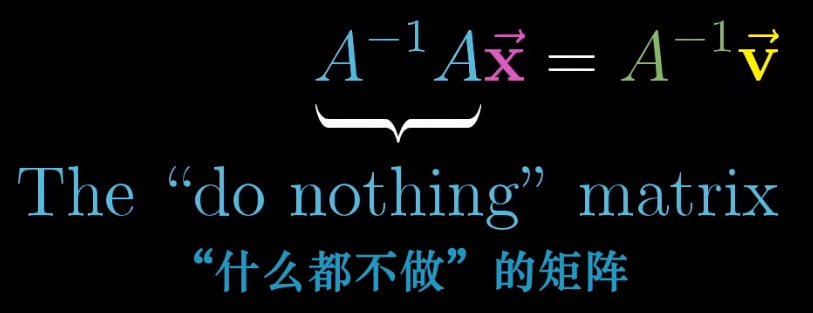本文已收录到:线性代数的本质学习笔记 专题
线性方程组
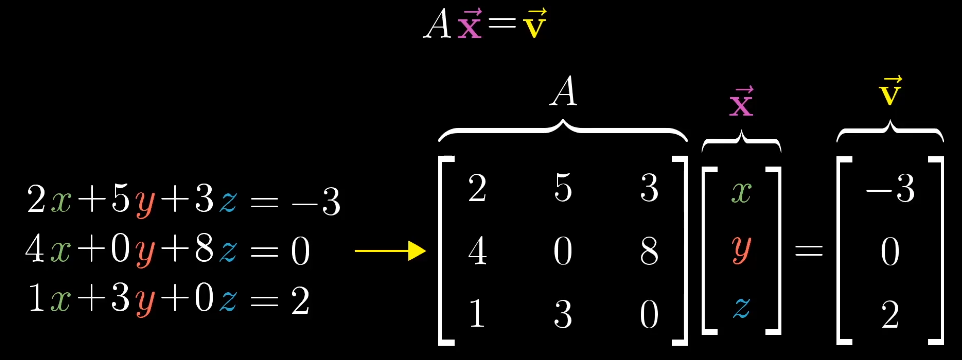
在每个方程组中,未知量只具有常系数,这些未知量之间只进行加和,没有幂次、没有函数等。这就被成为线性方程组。
线性方程组就是矩阵A和$\vec{x} $的乘积:A是系数,$\vec{x} $是向量,以及他们的乘积$\vec v$向量。
从几何的角度来思考,矩阵A表示一个线性变换(即记录下线性变换的操作),我们需要找到一个$\vec x$使得它在变换后和$\vec v$重合。
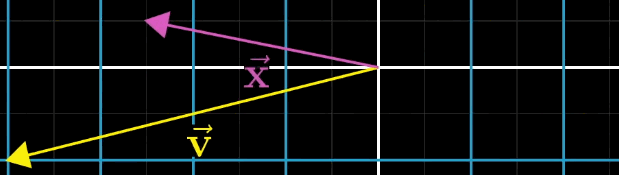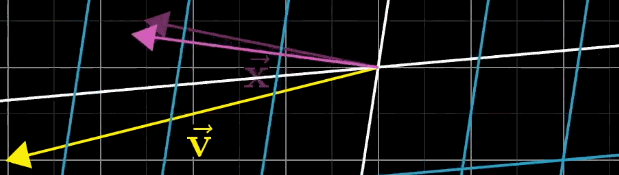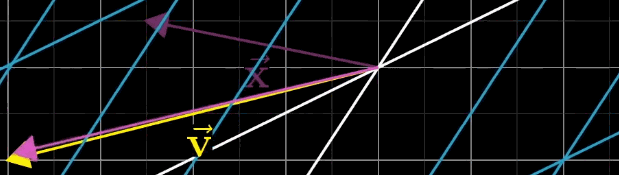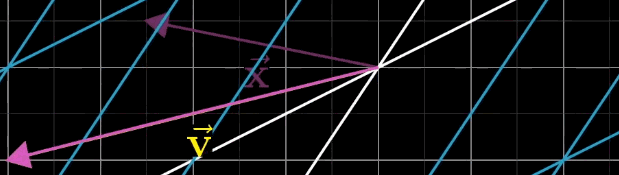
使用之前的几何直观来翻译个公式即$\vec{x} $经过 矩阵变换后,恰好落在$\vec v$向量上,如下图:
如何求 $\vec{x} $。逆向思考,从$\vec{v} $ 出发,进行某一个矩阵变换,恰好得到$\vec{x} $ 。而这个反过来的矩阵变换,就称为 矩阵的逆矩阵,写成公式是:
所以通过在A矩阵的左侧乘以一个A的逆矩阵就得到求解$\vec{x} $的方程。
伴随矩阵
弹幕:伴随就是不但把变化后的向量拉回到原向量的位置,还要把向量拉伸的再缩放回去,就等于是把一个向量的方向和大小都给它变回基向量的位置。
逆矩阵


线性方程组的解
对于方程组$A\vec x = \vec v$,线性变换A存在两种情况:
$det(A) =0$:空间被压缩到更低的维度,这时不存在逆变换,因为不能将一个直线解压缩为一个平面,这不是函数能做到的,压缩不可逆:
![]()
![]()
即使不存在逆变换,但解可能仍然存在,如果很巧,$\vec v$ 刚好落在压缩后的空间上:

$det(A) \neq0$:这时空间的维数并没有改变,有且只有一个向量经过线性变换后和$\vec v$重合。
秩
除了0行列式外,我们还有特殊的属于来描述上述“压缩”、“解压缩”、解的存在情况,即——秩。
秩为1:变换后的结果是一维的,也就是落在一条直线上
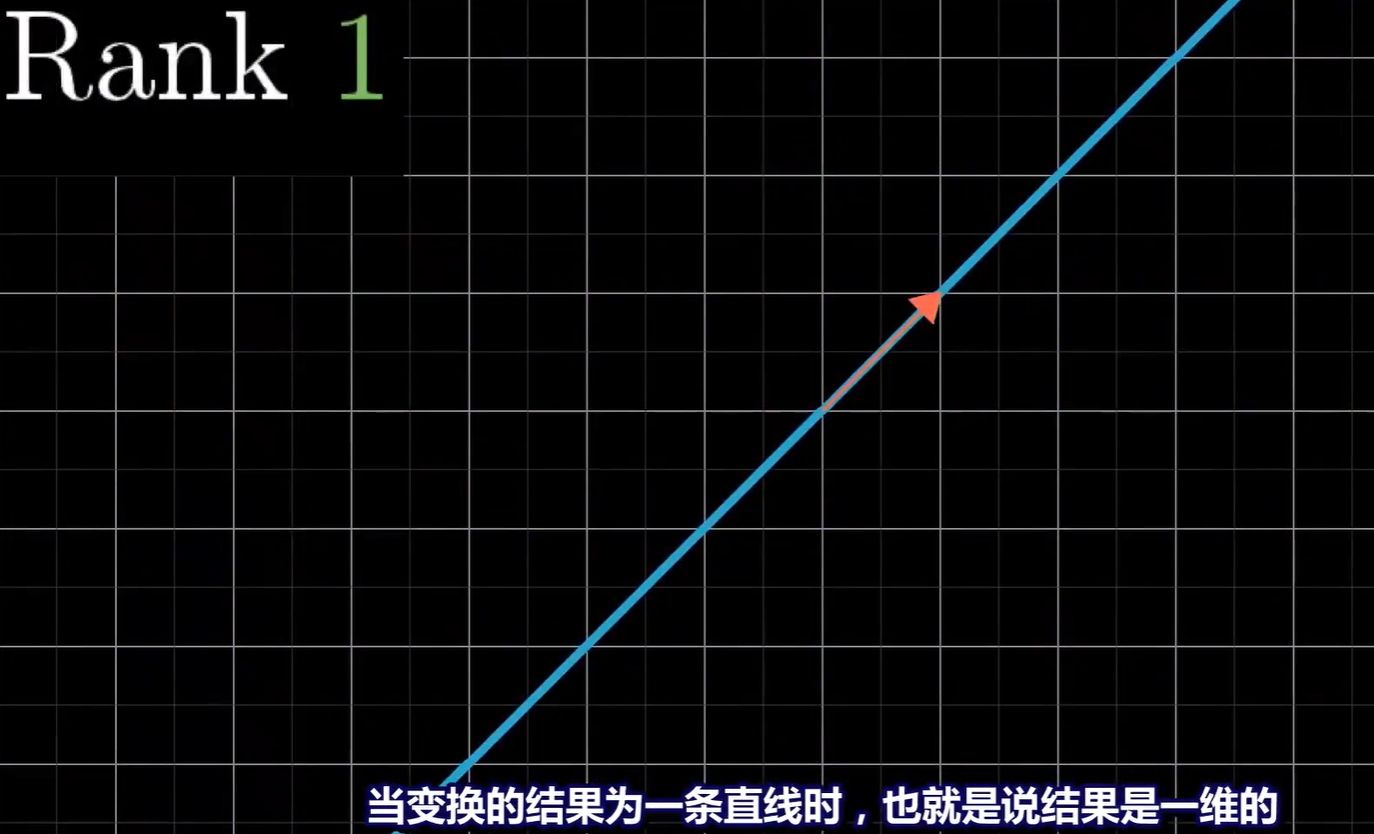
秩为2:变换后落在一个平面上
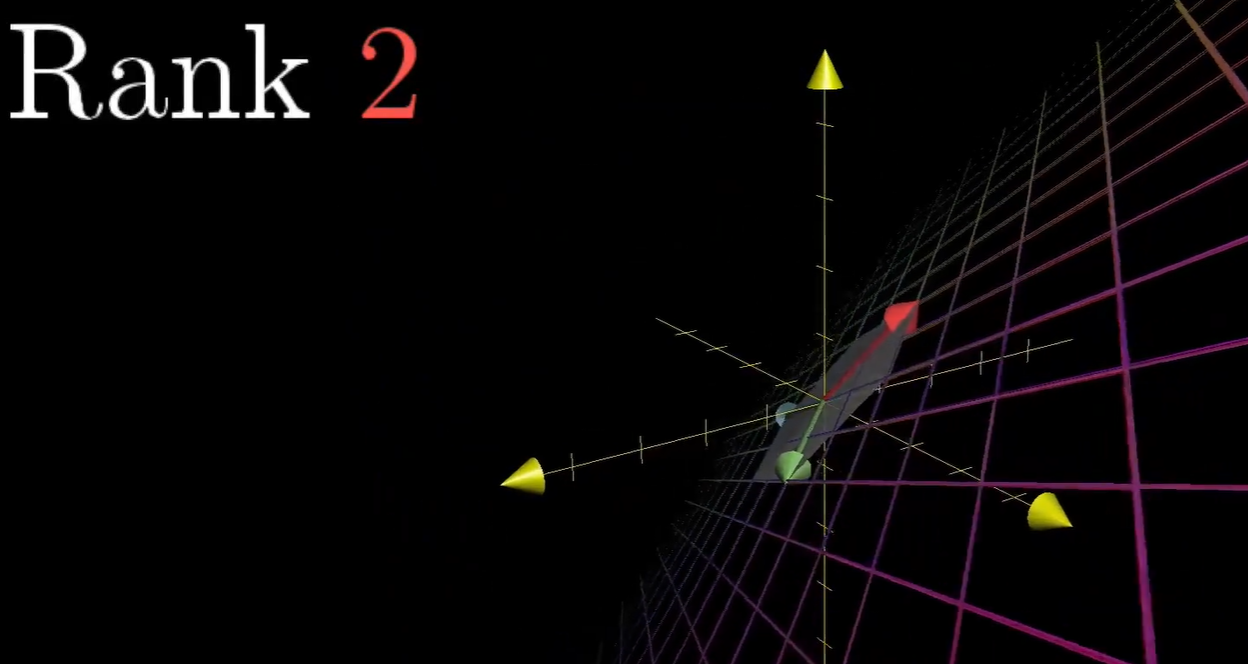
- 秩是线性无关向量个数,秩代表变换后空间的维数,其实叫做“维度”可能更容易来理解。
- 行列式只能判断空间是否压缩为0,而秩能判断压缩为几维。
列空间
不管是一条线、一个平面还是三维空间,所以可能变换的结果的集合被称为矩阵的列空间,即所有列向量张成的空间。所以秩更精确的定义是列空间的维数。
当秩达到最大值时,意味着秩与列数相等,成为满秩。
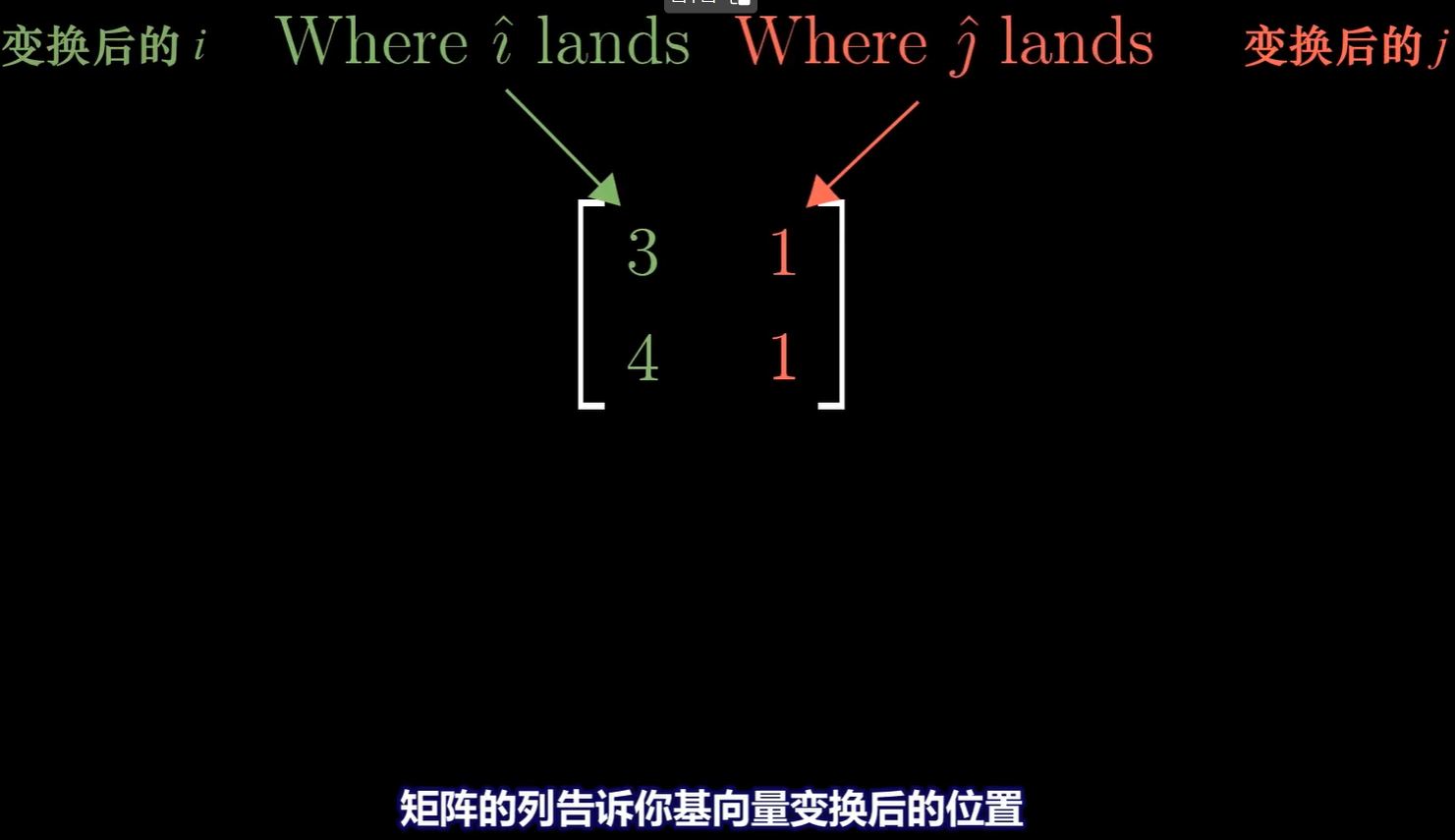
变换后基向量张成的空间就是所有可能的变换结果;列空间就是矩阵的列张成的空间。更精确的定义——秩是列空间的维数
零空间
- 图1:二维压缩到一个直线(一维),有一条直线(一维)的点被压缩到原点
- 图2:三维压缩到一个面(二维),有一条直线(一维)的点被压缩到原点
- 图3:三维压缩到一条线(一维),有一个面(二维)的点被压缩到原点
注意:压缩就是变换,变换就是矩阵,其实说的就是矩阵
变换后落在原点上的向量的集合称为矩阵的零空间或核。
当$A\vec x = \vec v$中的$\vec v$是一个零向量,即$A\vec x = \begin{bmatrix}0 \\0\end{bmatrix}$时,零空间就是它所有可能的解。
这就是基础解系,而特解就是在变换后得到的直线空间上找的向量;
这里对应齐次方程组解的两种情况;这也解释了,为什么齐次线性方程组在系数矩阵不满秩的时候有无穷姐解;
压缩后在列空间内,说明之前就在原空间内,所以有解。而不在压缩后的空间内,说明原本就不在与原空间内,自然无解。;
AX=V,V经过A的变换后,如果落在A组成的列空间内,则有解,否则无解
总结
- 每个方程组都有一个线性变换与之联系,当逆变换存在时就可以利用逆变换求解方程组;
- 列空间可以让你知道什么时候存在解;
- 当$\vec v$恰好为0时,零空间给出的就是这个向量方程所有可能的解。
非方阵
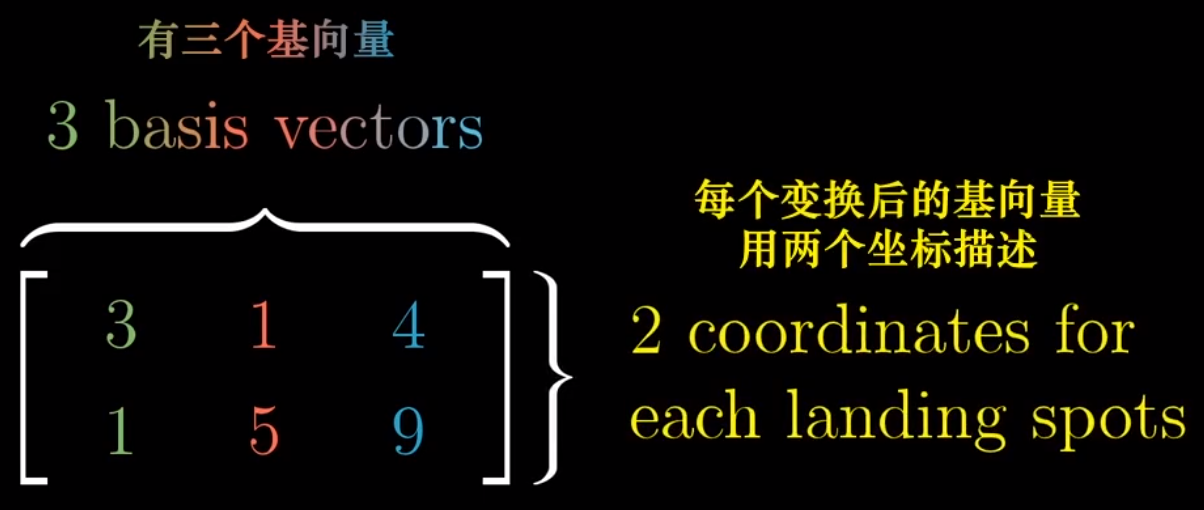
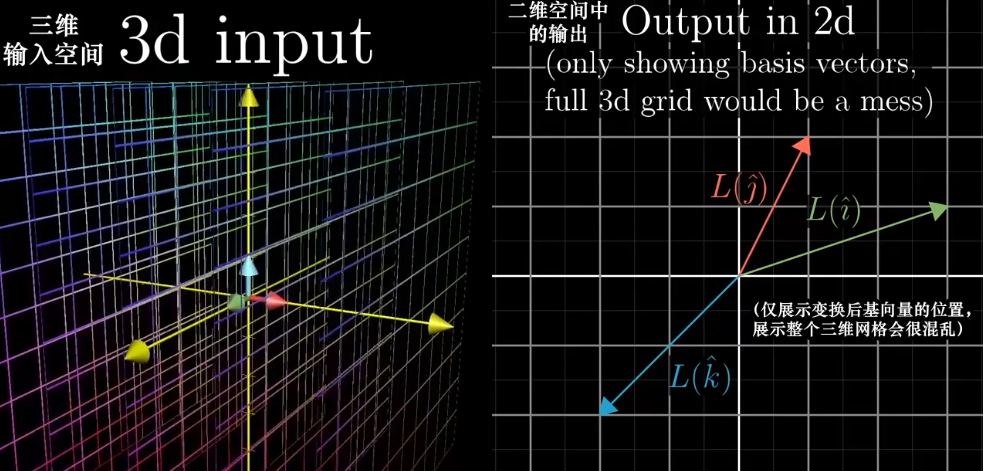
几何意义
Ps:没有升维,这是三维空间中的二维子空间。
即这是三维空间中的二维平面。
三维空间映射到二维空间:上图3×2的矩阵表示将一个三维空间映射到二维空间上。
二维空间映射到一维空间:一个$1\times 2$的矩阵:$\begin{bmatrix}1&2 \end{bmatrix}$表示一个二维空间映射到一维空间。
弹幕:与其说是降维,不如说是3D空间在2D空间的“投影”,就像手电筒照射物体投影在墙面一样。
总结:
非方阵乘法、非方阵行列式
【直观详解】线性代数的本质 | Go Further | Stay Hungry, Stay Foolish (charlesliuyx.github.io)
参考文献:【直观详解】线性代数的本质 | Go Further | Stay Hungry, Stay Foolish (charlesliuyx.github.io)