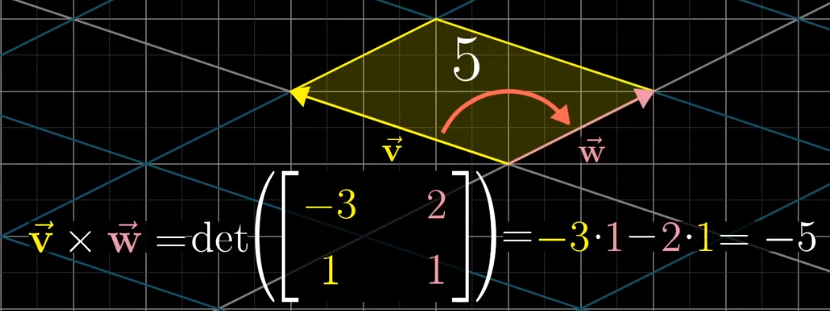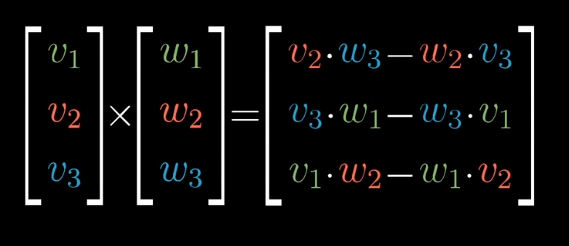本文已收录到:线性代数的本质学习笔记 专题
文章目录
隐藏
叉积的几何意义
对于两个向量所围成的面积来说,可以使用行列式计算,即将两个向量看作是变换后的基向量,这样通过行列式就可以得到变换后面积缩放的比例,因为基向量的单位为1,所以就得到了对应的面积。
这个面积的值存在负值,这是参照基向量$\vec i$和$\vec j$的相对位置来说的:
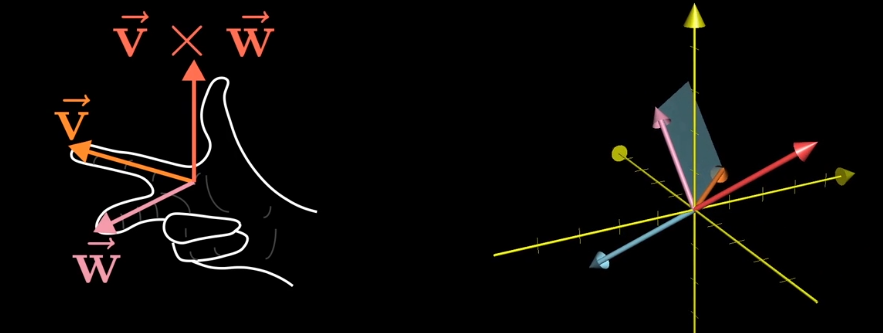
叉积是通过两个三维向量$\vec v$和$\vec w$,生成一个新的三维向量$\vec u$,这个向量垂直于向量$\vec v$和$\vec w$所在的平面,长度等于它们围成的面积。
叉积的方向可以通过右手定则判断,即右手大拇指指向的方向是叉积的方向:
叉积的计算
这乍一看非常奇怪,但是它可以由一个三行行列式代替。使得这种运算更加简便。
第一次学这个计算方法的时候,估计没几个人能想清楚它为什么是这样的形式,甚至老师也说不清,只是告诉学生,我们这么记下来,定义是这样的定义的。但是,既然是直观讲解,必须把这里的来由探明清楚。
以线性变换的角度看叉积