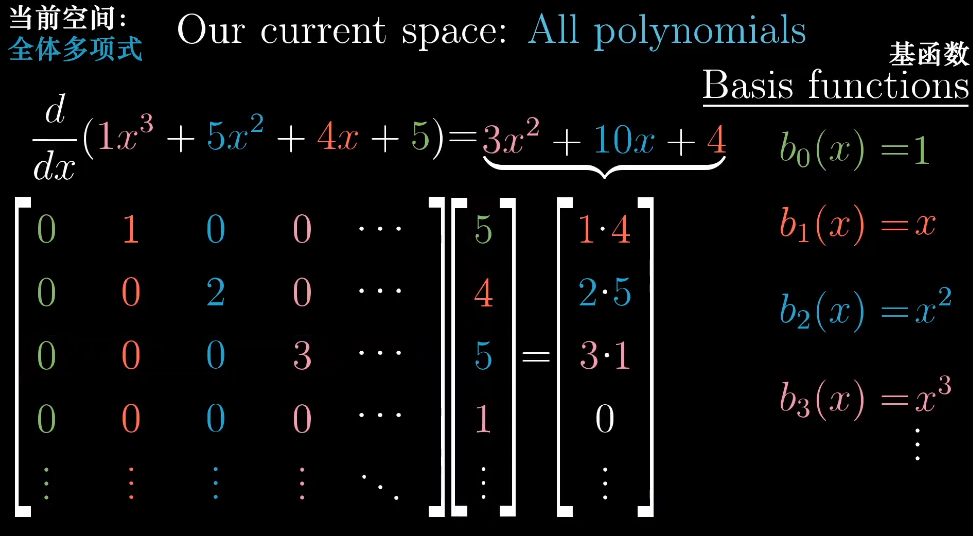本文已收录到:线性代数的本质学习笔记 专题
函数与向量
这里的内容对应的就是线性代数中的二次型。
先看一个例子,因为求导的可加性和成比例性,我们可以分别对每个基向量求导,从而得到左侧的矩阵:
弹幕:用泰勒展开所有的函数成幂函数,然后用这个算子,就可以解决几乎所有的函数。
如上图,以取 的不同幂次方作为基函数,然后既可以写出求导变换的矩阵。这更进一步佐证了开篇提到的关键句子,矩阵 = 变换的数字表达
| 线性代数 | 函数 |
|---|---|
| 线性变换 | 线性算子 |
| 点积 | 内积 |
| 特征向量 | 特征函数 |
有很多类似向量的不同事物,只要你处理的对象具有合理的数乘和相加的概念,线性代数中所有关于向量,线性变换和其他的概念都应该使用与它。作为数学家,你可能希望你发现的规律不只对一个特殊情况适用,对其他类似向量的事物都有普适性。
向量空间
这些类似向量的事物,比如箭头、一组数、函数等,他们构成的集合被称为:向量空间
向量加法和向量数乘的规则 – 被称为公理,如下图:
这些公理是一种媒介,用来连接数学家和所有想要把这些结论应用于新的向量空间的人。——这里有点像变成里面的interface或者接口、函数参数的概念。
作为数学家,你也不必考虑人们定义的所有可能的、奇怪的向量空间了。你只需要根据这些公理(接口、参数)去证明你的结论。所以根据这些公理描述一个空间,而不是集中于某一个特定的向量上。简而言之,这就是为什么你阅读的每一本教科书都会根据可加性和成比例来定义线性变换。
所以,对于向量是什么这个问题,数学家会直接忽略不作答。向量的形式并不重要,只要相加和数乘的概念遵守八条公理即可。