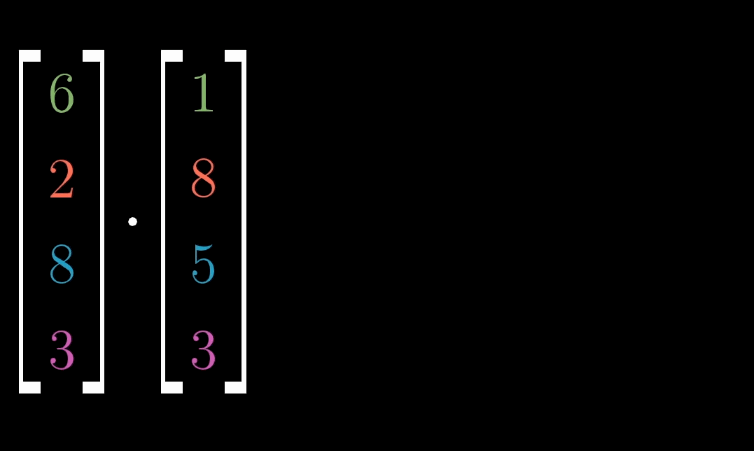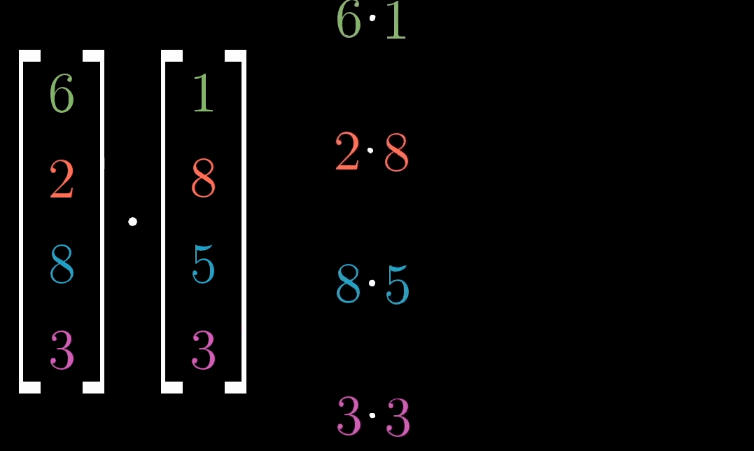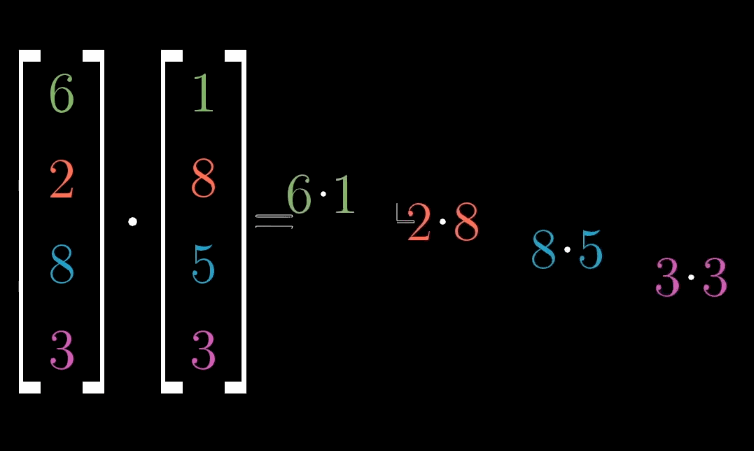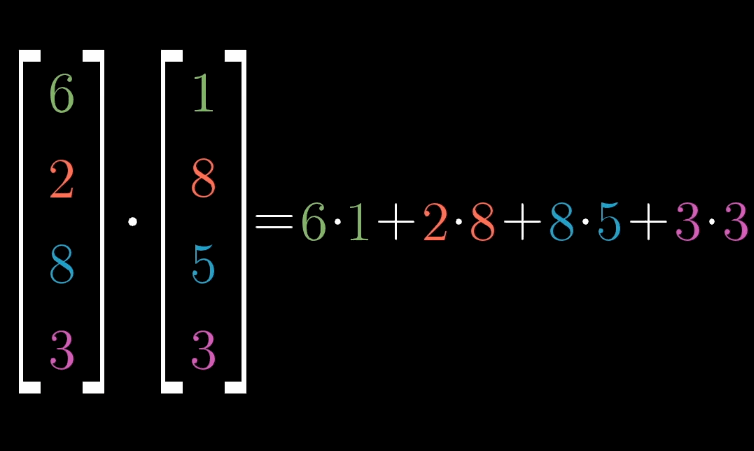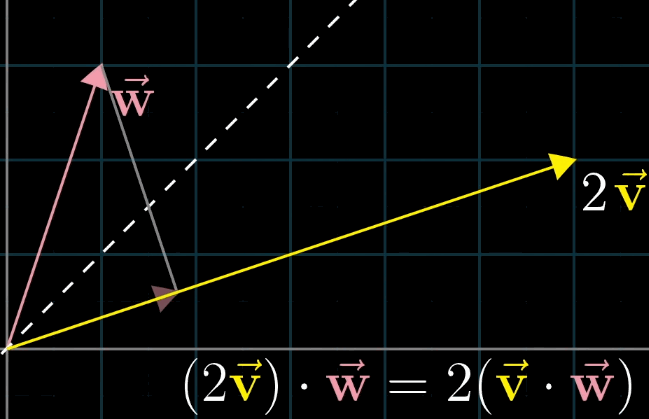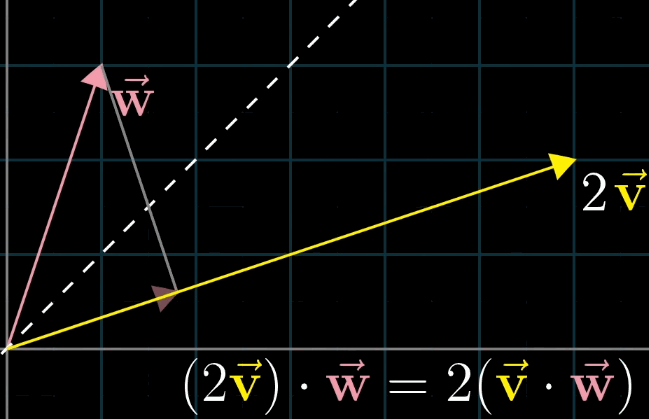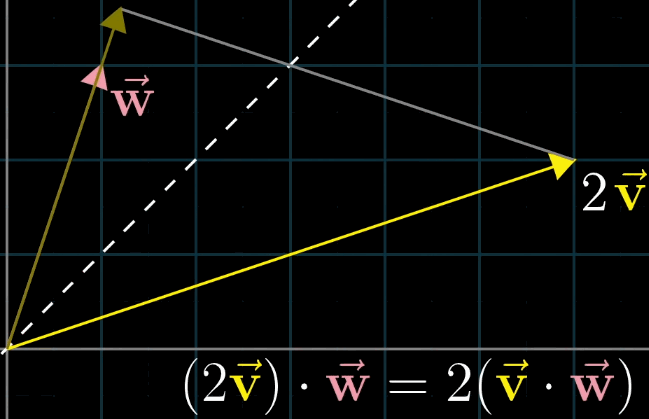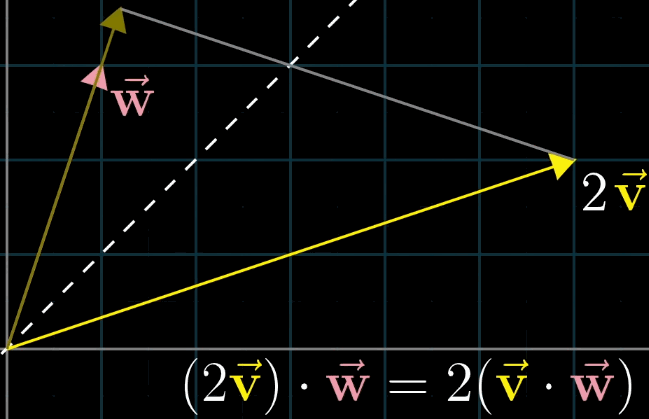本文已收录到:线性代数的本质学习笔记 专题
点积(又称数量积或标量积)的计算
对于两个维度相同的向量,他们的点积计算为:$\begin{bmatrix}1\\2\end{bmatrix}\cdot\begin{bmatrix} 3\\4\end{bmatrix}=1\cdot3+2\cdot4=11$。
Ps:高中数学向量乘积一般都是点乘,叉乘是高数才会教。
点积的几何解释
几何直观来说,$\vec{v}$可以想象成向量$\vec{w}$ 朝着过原点和向量$\vec{v}$的直线上的正交(垂直)投影,然后把投影的长度和向量 $\vec{v}$的长度乘起来就是点击的值。其中正负号代表方向,两个向量成锐角大于0;钝角小于0。
如果$\vec{w}$的投影与$\vec{v}$方向相反的话,点积为负值:
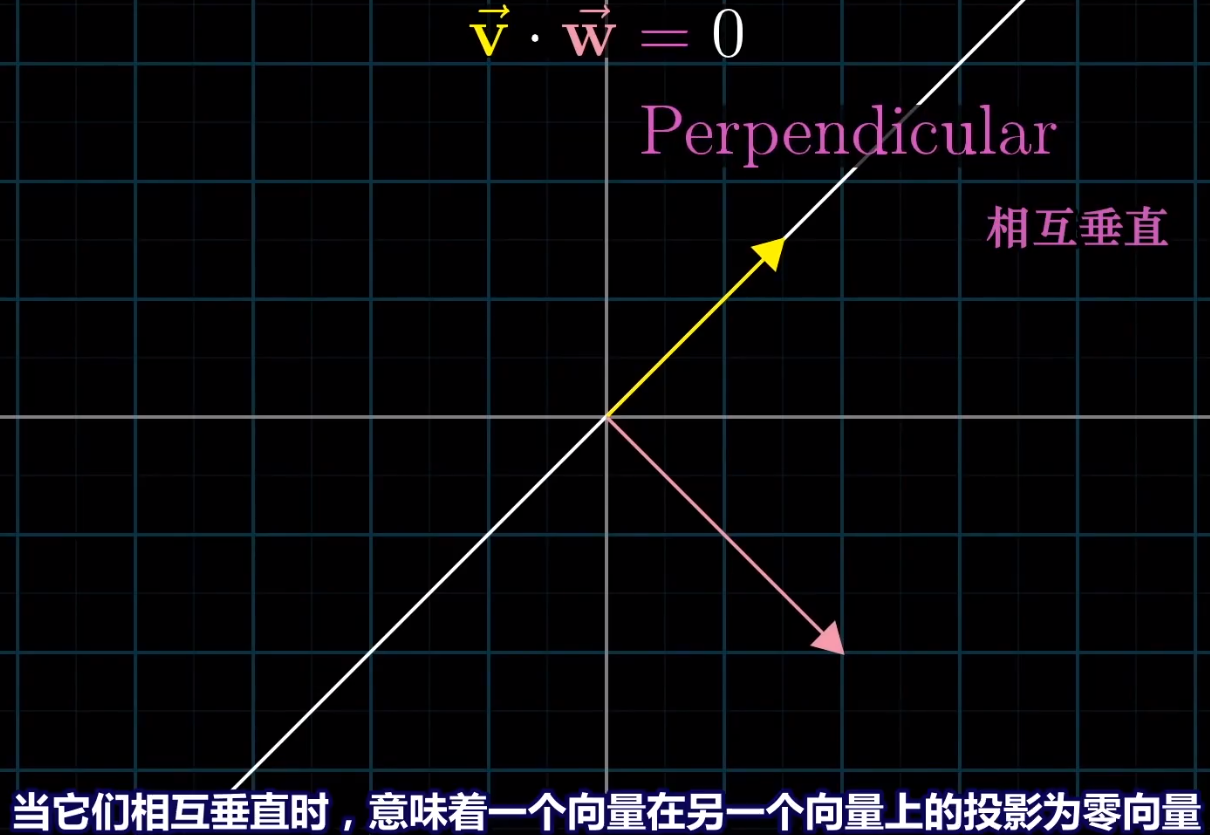
当$\vec{w}$的投影与$\vec{v}$方向垂直的话,点积为0:
点积的顺序
你可能会觉得,顺序在线性代数其实是很重要的,而对于$\vec{v}$和 $\vec{w}$它们的结果却是相同的,为什么呢?
解释的方法为:首先假设 $\vec{v}$ 和$\vec{w}$长度相同,利用对称轴,两个向量互相的投影相等;接下来如果你缩放其中一个到原来的两倍,对称性则被破坏,但是缩放比例没变,最终乘法的结果也没变:
可以通过相似三角形来理解:
点积与投影——解释为什么点积是这样运算的
为什么点积和坐标相乘联系起来了?这和对偶性有关。
对偶性
对偶性的思想是:每当看到一个多维空间到数轴上的线性变换时,他都与空间中的唯一一个向量对应,也就是说使用线性变换和与这个向量点乘等价。这个向量也叫做线性变换的对偶向量。
例如:
当二维空间向一维空间映射时,如果在二维空间中等距分布的点在变换后还是等距分布的,那么这种变换就是线性的:
但如果像下面这样变化,那么变换后就不是等距的:

假设有一个线性变换A$\begin{bmatrix}1&-2\end{bmatrix}$和一个向量$\vec v=\begin{bmatrix}4\\3\end{bmatrix}$。变换后的位置为$\begin{bmatrix}1&-2\end{bmatrix}\begin{bmatrix}4\\3\end{bmatrix}=4\cdot1+3\cdot-2=-2$,这个变换是一个二维空间向一维空间的变化,所以变换后的结果为一个坐标值。我们可以看到线性变换的计算过程和向量的点积相同$\begin{bmatrix}1\\-2\end{bmatrix}\cdot\begin{bmatrix}4\\3\end{bmatrix}=4\cdot1+3\cdot-2=-2$,所以向量和一个线性变化有着微妙的联系。
总结上图:将向量转换为数的线性变化(即矩阵)和这个向量本身有着某种联系。也就是矩阵可由若干向量组成。
弹幕:矩阵与向量,在外观上类似,但表达的含义不同。矩阵代表变换,向量代表空间
推广开:
后面视频讲的非常精彩,移步:【-UP主汉语配音-【线性代数的本质】合集-转载于3Blue1Brown官方双语】】 【精准空降到 07:16】 https://www.bilibili.com/video/BV1ib411t7YR/?p=10&share_source=copy_web&vd_source=8387734dc2ae5c1793399ea83221d291&t=436
对偶性是指两种看似毫不相关的概念竟然天然的有着联系,这个在数学中也很常见。