本文已收录到:线性代数的本质学习笔记 专题
什么是特征值和特征向量
对于一些线性变化来说,存在一些向量在变换前后留在了张成的空间里,只是拉伸或收缩了一定比例,这些向量称为特征向量,拉伸收缩的比例称为特征值,正负表示变换的过程中是否切翻转了方向。
例如下图,红色的向量变换前后都在一条直线上,而蓝色的向量变换前后不在一条直线上:
- 变换中被留在张成空间内的向量,就是特征向量。
- 其中每个向量被拉伸或抽缩的比例因子,就是特征值。
- 正负表示变换的过程中是否切翻转了方向。
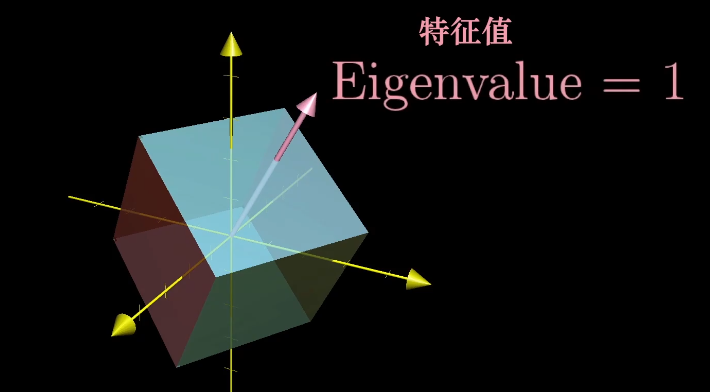
例如一个三维空间的旋转,如果能找到特征值为1的特征向量,那么它就是旋转轴,因为旋转并不进行缩放,且旋转轴在线性变换中保持不变。
求解特征向量和特征值
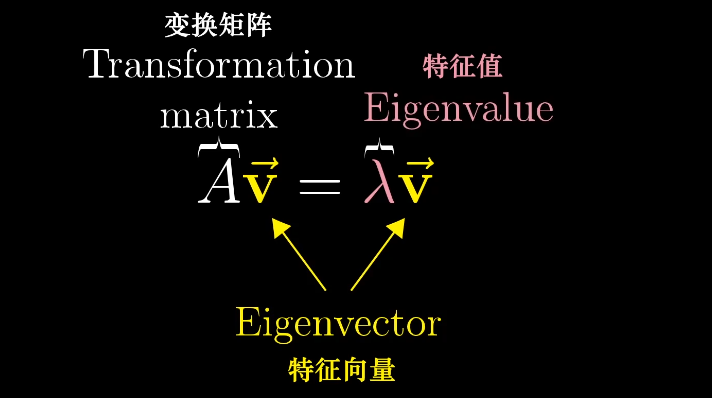
特征向量的概念,等号左侧表示矩阵向量的乘积,等号右侧表示向量数乘,可以将右侧重写为某个向量的乘积,$\vec I$为单位向量:
通过改写,变成了求解线性方程组的形式:
现在我们得到了新的矩阵:$A-\lambda I$。我们的任务是求解$\vec v$。观察这个等式你会发现:可以把$A−\lambda I$矩阵看成一个对$\vec{v} $矩阵的变换,目的是把$\vec{v} $压缩到更低的维度。而空间压缩对应的恰好就是变换矩阵的行列式为0。
举个具体的例子:
几种特殊的二维变换
旋转变换
解出特征值能发现答案是虚数 ,没有特征向量存在,即特征值出现复数的情况一般对应于变换中的某种旋转。
剪切变换
剪切变换,x轴不变,他的特征向量不够多,只有一个特征值,为1。(因为)
伸缩变换
特征值只有一个,但是是空间中所有的向量都是特征向量。
特征基
如果所有的基向量都是特征向量,那么它对应的矩阵是一个对角矩阵,矩阵的对角元是它们所属的特征值。
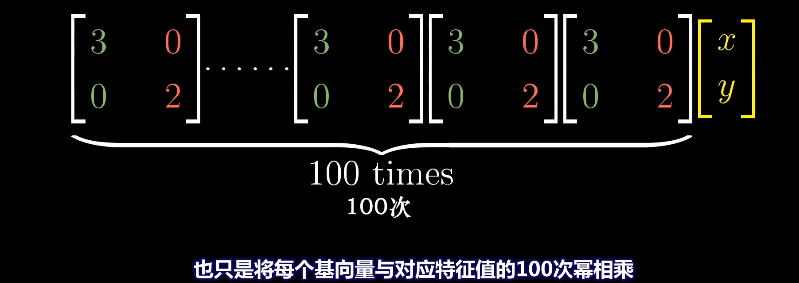
对角矩阵在求幂次时可以更方便求解,对应的幂次就是对角元的幂次。而对于非对角矩阵的幂次求解就非常麻烦。
在实际中,我们遇到对角矩阵的概率很低,但是我们可以通过基坐标变换来得到对角矩阵(矩阵的相似对角化),前提有足够多的特征向量且可以张成整个空间,例如剪切变化就不行,应为它只有一个特征向量,无法进行坐标变换。