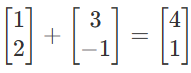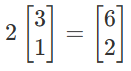本文已收录到:线性代数的本质学习笔记 专题
前言
在笔记开始之前,想象学习一个事物(概念)的场景:我们需要学习正弦函数,,非常不幸的是,你遇到了一本相当装逼的教材,它告诉你,正弦函数是这样的: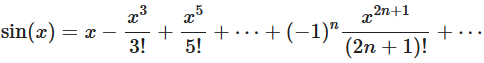
的确很厉害的样子,并且,计算器就是这样算 ,知道了这个的确“挺酷的”。对你来说,你的作业可能就是回家把 带到公式里面,发现,好神奇!竟然越算越接近0.5。此时你对与三角形之间的几何直观只有一些模糊的概念。这样的学习过程就十分悲催了。为什么呢?
再假设一个场景,接下来,物理课,正弦函数随处可见,下图场景中,其他人能快速的大概估计出这个值是0.7。而刚“学过”正弦函数的你,内心戏可能是这样的:这些人太厉害了吧
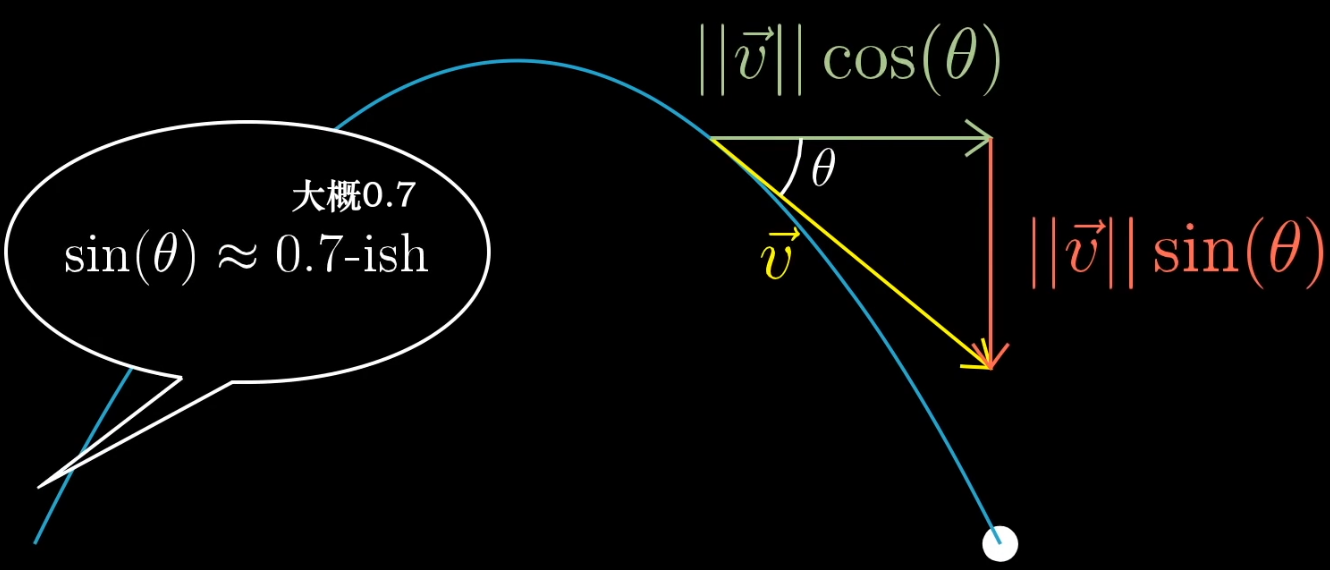
你可能会觉得这些做物理的人脑子也太强了,我弱爆了。其实,你需要只是一个几何直观的灌输而已,这也从侧面佐证了一个好的老师是有多么重要。
教学不同层次的人:初学,入门,掌握,理解,都是不同的。解释的角度,方式都完全不同。更加不幸的是,为了能更加通用的用理论来描述现实生活中的规律,人类已经做了很多工作,我们常说:越通用,越抽象(越难以理解)。这对于初学者来说堪称一段噩梦。
这个例子比较极端,但只为强调一件事:直观理解很重要,或者说,学习方法很重要。好的学习方法即你如何直观的去理解(可能是几何的,或是现实中的具体例子)一个抽象的事物,并层次化的建立知识与知识间的联系,构建并健壮属于自己的知识图谱。个人观点是,这种学习方法是最高效的。它唯一的难度在于,需要一定的基础知识打底,一定的量变结合方法论(点拨或领悟)就是质变。
根据生物学家我们知道,人对具体的事物(动画>图形>数字>未建立直观理解的文字)更敏感,记忆速度更快。这篇笔记的对象3B1B团队生产的内容目的就是从为了帮助人们建立直观概念的角度来教学,在如今中国应试教育风行的大背景下,它会超越你的认知:学习如追番般期待,真不是一个调侃!
我是极度反对现代大学的线性代数课程中(甚至数学类课程)的教学方法的,在计算上(应试做题)花费了大量时间。而工程中,有计算机,绝不会有任何一个人去笔算矩阵的逆或特征值。如果现在的老师反驳:做计算的目的是为了让你通过大量的联系(重复)去记牢概念,我也一直坚信:学习知识的最快捷径是带有思考的重复,但那是带思考的重复,有一些直观的方法在帮助你理解和记忆上比做题有效率的多。
向量究竟是什么
向量对于不同的学科有不一样的定义。
物理中的向量是空间中箭头,由长度和方向决定,长度和方向不变,向量可以随意移动,它们表示的是同一个向量。是二维的。
- 向量是空间中的箭头
- 决定一个向量的是:它的长度和它所指的方向
计算机中的向量更多的是对数据的抽象,可以根据面积和价格定义一个房子$\begin{bmatrix}100m^2\\700000¥\end{bmatrix}$。第一个数字代表房屋的面积,第二个数字代表价格。这里的顺序不可以颠倒。向量是列表的另一种说法。
- 向量是有序的数字列表
- 向量不过是“列表”一个花哨的说法
- 向量的维度等于“列表”的长度
从数学来说,它的本质就是通用和抽象,所以,数学家希望概括这两种观点
- 向量可以是任何东西,只需要保证:两个向量相加及数字与向量相乘是有意义的即可
- 向量加法和向量乘法贯穿线性代数始终,十分重要
坐标系与向量的基本运算
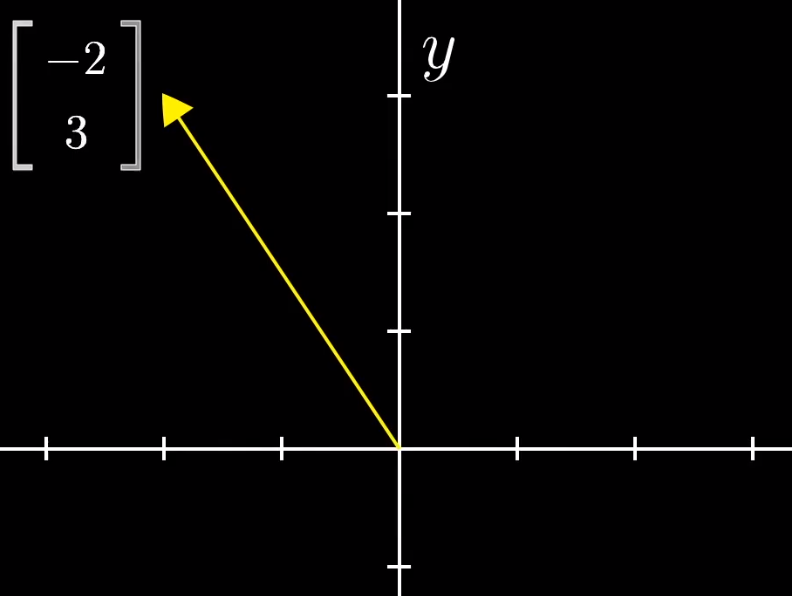
把向量至于坐标系中,坐标正负表示方向,原点(向量起点)为起点。
一对向量坐标由一对数表示,这对数指导着你如何从向量原点出发到达向量终点。
第一个数代表应沿着x轴走多远,正数代表朝着x轴正向移动,负数代表相反。
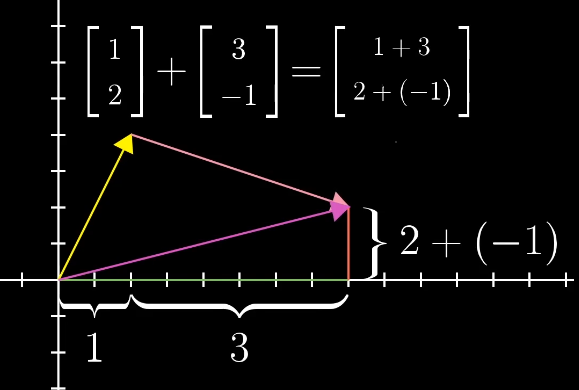
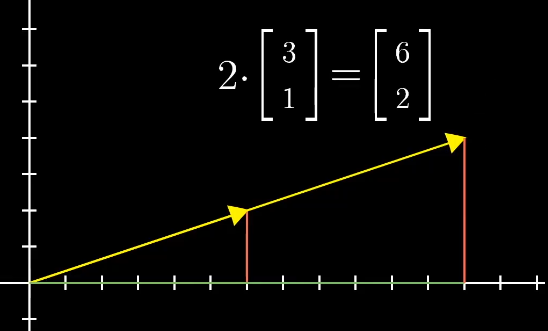
向量的加法:可以理解为在坐标中两个向量的移动。即向右移动1+3步,再向上移动2+(-1)步:
即:
- 向量加法
- 物理角度:运动
- 数字角度:坐标相加
- 向量乘法
- 物理角度:缩放
- 数字角度:坐标和比例相乘
标量:缩放的倍数,即向量前面的数字。
线性组合:张成的空间与基
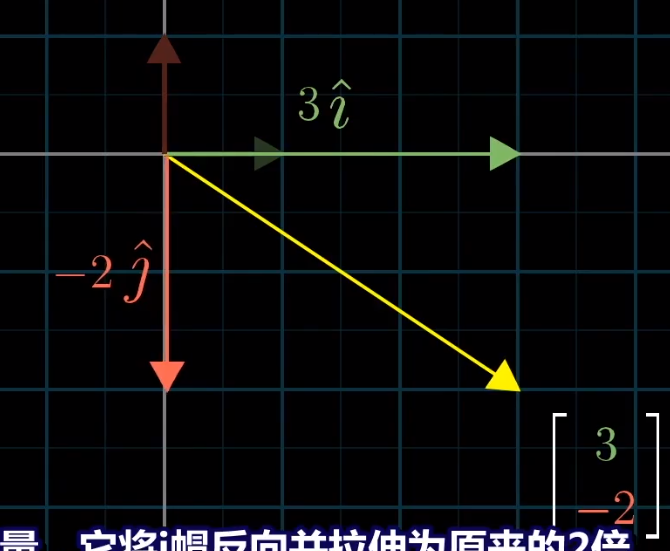
所以下面的向量可以认为是i向量拉伸为原来的三倍,j向量拉伸为原来的-2倍:
不仅仅如此,基向量没有要求必须是x轴和y轴的一个单位。事实上,空间中的任何两个不共线的向量都可以看作基向量。
每当我们用数字描述向量时,他都依赖于我们正在使用的基。
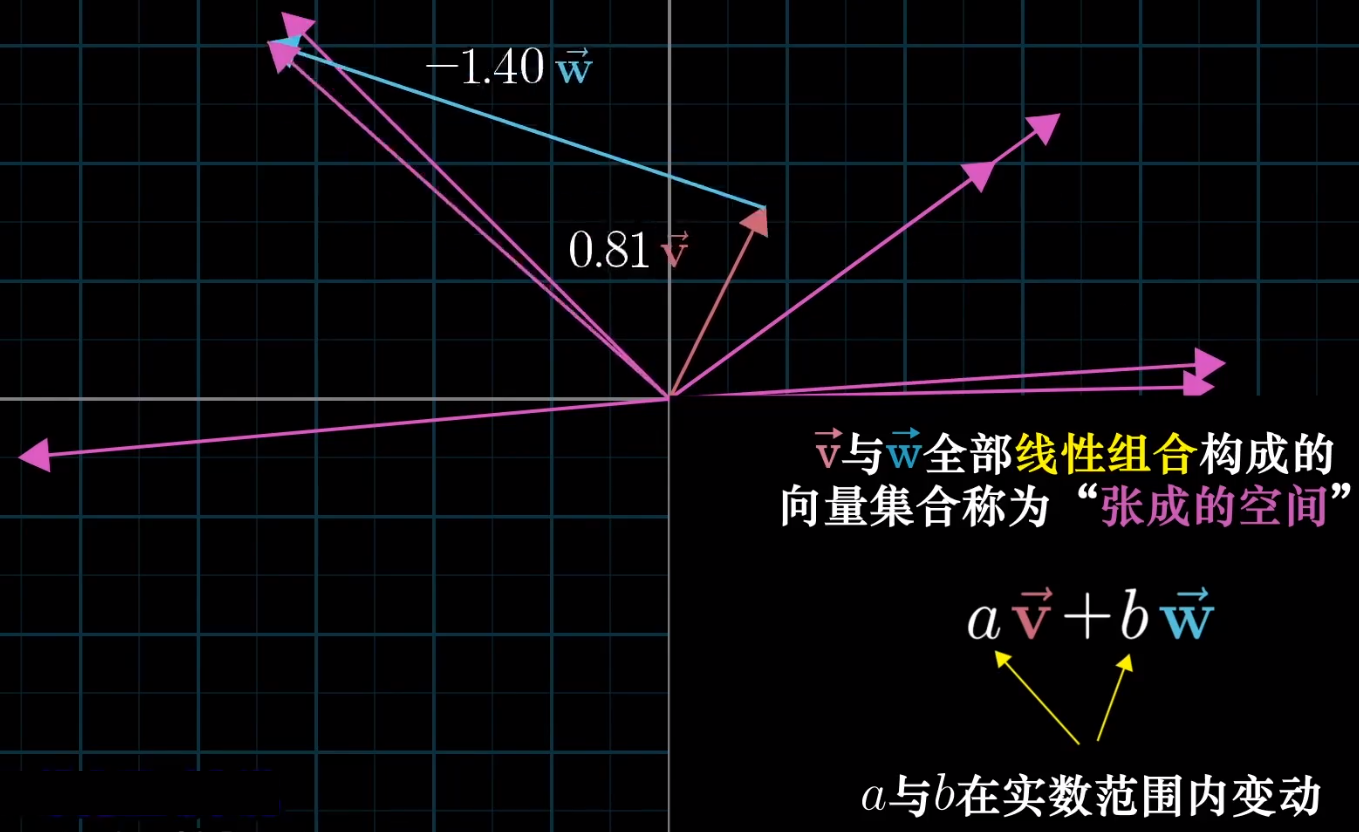
线性组合
- 两个数乘向量称为两个向量的线性组合$$a\vec v+ b\vec w$$。
- 第一种可能:两个不共线的向量通过不同的线性组合可以得到二维平面中的所有向量。
- 第二种可能:个共线的向量通过线程组合只能得到一个直线的所有向量。
- 第三种可能:如果两个向量都是零向量那么它只能在原点。
张成的空间(即:扩展成的空间)
当你只考虑一个向量时,就把它看成箭头;当考虑多个向量时,就把他们都看作点。
所有可以表示给定向量线性组合的向量的集合称为给定向量的张成空间(span)。
一般来说两个向量张成空间可以是直线(固定一个向量)、平面(两个向量都可以伸缩)。
三个向量张成空间可以是平面、空间。
如果多个向量,并且可以移除其中一个而不减小张成空间,那么它们是线性相关的,也可以说一个向量可以表示为其他向量的线性组合$$\vec u = a \vec v + b\vec w$$。
如果所有的向量都给张成的空间增加了新的维度,它们就成为线性无关的$$\vec u \neq a \vec v + b\vec w$$。