本文已收录到:人工智能实践:Tensorflow笔记 专题
人工智能三学派
本讲目标:学会神经网络计算过程,使用基于TF2原生代码搭建你的第一个的神经网络训练模型
当今人工智能主流方向——连接 主义
- 前向传播
- 损失函数(初体会)
- 梯度下降(初体会)
- 学习率(初体会)
- 反向传播更新参数
人工智能:让机器具备人的思维和意识。
人工智能三学派:
- 行为主义:基于控制论,构建感知-动作控制系统。 (控制论,如平衡、行走、避障等自适应控制系统)
- 符号主义:基于算数逻辑表达式,求解问题时先把问题描述为表达式,再求解表达式。(可用公式描述、实现理性思维,如专家系统)理性思维
- 连接主义:仿生学,模仿神经元连接关系。(仿脑神经元连接,实现感性思维,如神经网络)感性思维
理解:基于连结主义的神经网络设计过程
用计算机仿出神经网络连接关系,让计算机具备感性思维。
- 准备数据:采集大量”特征标签”数据
- 搭建网络:搭建神经网络结构
- 优化参数:训练网络获取最佳参数(反传)
- 应用网络:将网络保存为模型,输入新数据,输出分类或预测结果(前传)
神经网络设计过程
给鸢尾花分类(lris)
- 0狗尾草鸢尾
- 1杂色鸢尾
- 2弗吉尼亚鸢尾
人们通过经验总结出了规律:通过测量花的花曹长、花尊宽、花瓣长、花瓣宽,可以得出鸢尾花的类别。
聪明的你会想到使用 if … case 语句来实现,其实这就是专家系统,把专家的经验告知计算机,计算机执行逻辑判别(这是一个纯理性思维计算),给出分类。
但是一个有着丰富经验的人不会这么刻板的去区分鸢尾花的类别。而是会像下面这样:
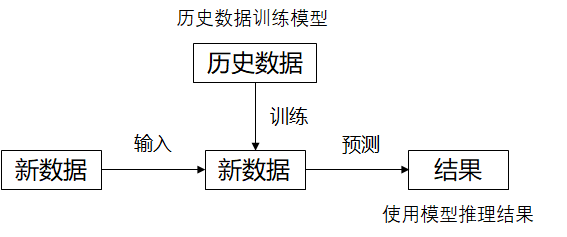
神经网络:采集大量(输入特征:花萼长、花夢宽、花瓣长、花瓣宽,标签(需人工 标定):对应的类别)数据对构成数据集。
把数据集限入搭建好的神经网络结构,网络优化参 数得到模型,模型读入新输入特征,输出识别
用神经网络实现鸢尾花分类:搭建网络
这里我们引入了MP模型,之前在机器学习中也讲述过。 –> 人工神经网络(ANN)及BP算法原理
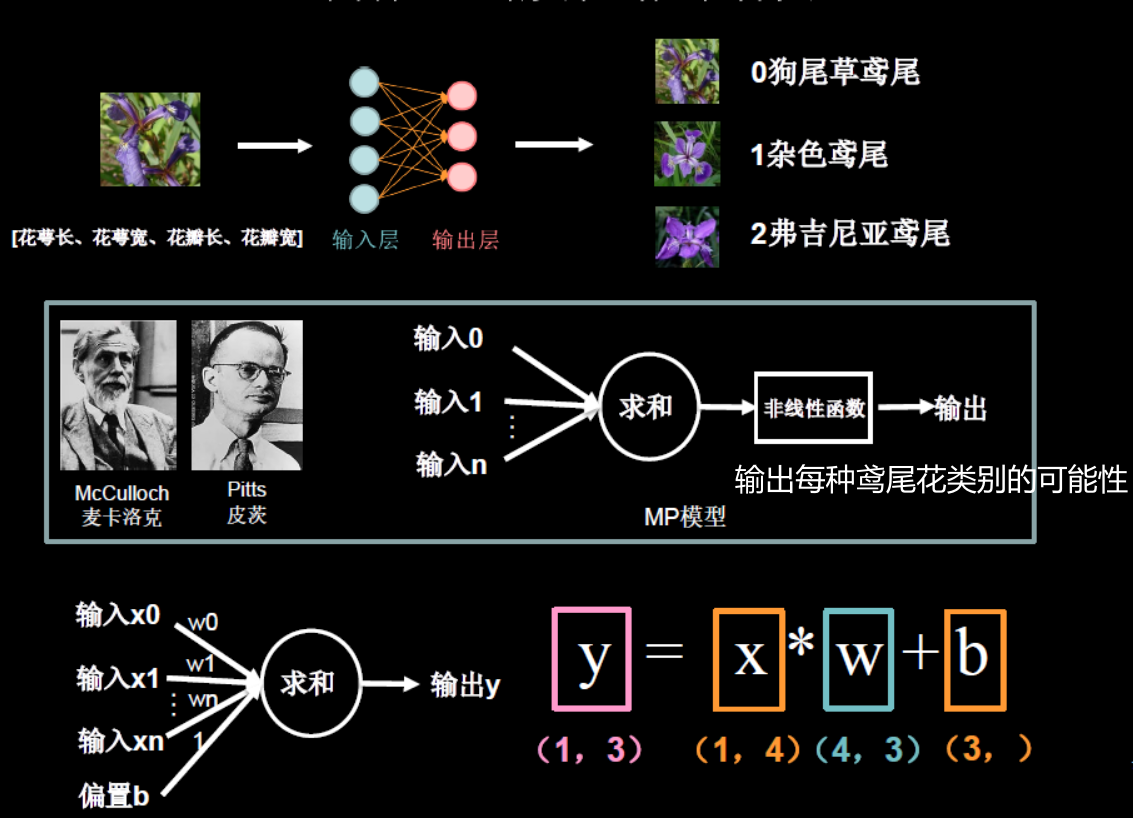
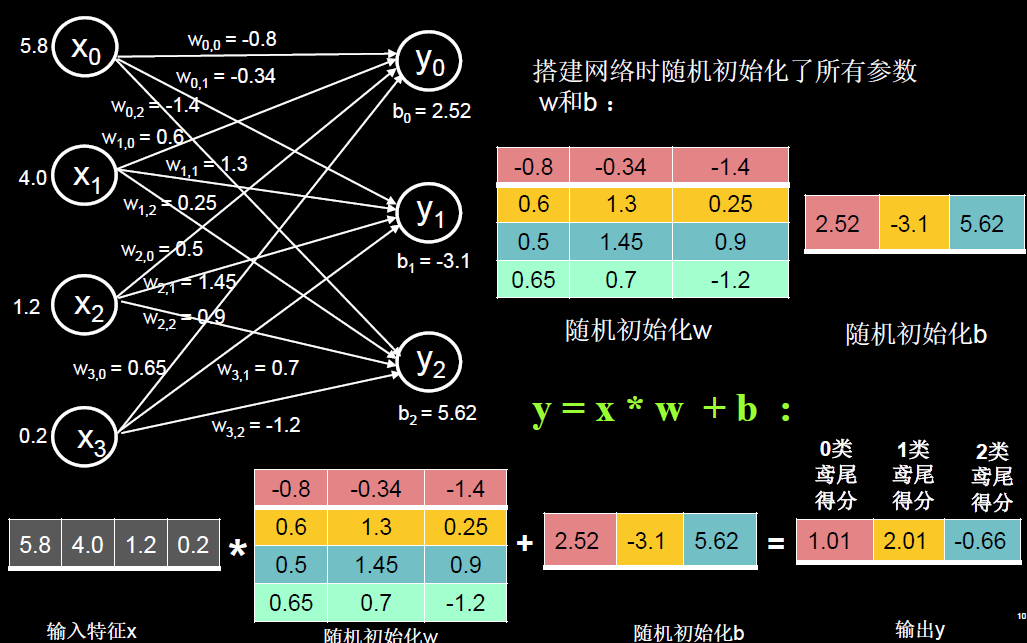
针对鸢尾花的例子:
- x是1行4列的输入特征,即花萼长、花萼宽、花瓣长、花瓣宽。
- w是这些线上的权重,是4行3列的。
- b是偏执,每个列各有一个。
下面的网络是全连接网络,w和b会被随机初始化。
该输入特征真实的分类是0类鸢尾花,即狗尾草鸢尾花。但是最终输出的得分y0类鸢尾花并不是最大的。这是因为我们最初的w和b是瞎糊弄的。
代码:
import tensorflow as tf
x1 = tf.constant([[5.8, 4.0, 1.2, 0.2]]) # 5.8,4.0,1.2,0.2(0)
w1 = tf.constant([[-0.8, -0.34, -1.4],
[0.6, 1.3, 0.25],
[0.5, 1.45, 0.9],
[0.65, 0.7, -1.2]])
b1 = tf.constant([2.52, -3.1, 5.62])
y = tf.matmul(x1, w1) + b1
# 显示几行几列
print("x1的shape:", x1.shape)
print("w1的shape:", w1.shape)
print("b1的shape:", b1.shape)
print("y的shape:", y.shape)
# 计算结果
print("y的值:", y)
用神经网络实现鸢尾花分类:损失函数
损失函数(loss function) :预测值(y)与标准答案(y_ )的差距。
损失函数可以定量判断W、b的优劣,当损失函数输出最小时,参数w、b会出现最优值。
损失函数有很多,下面的均方误差就是其中的一种。
均方误差: $$ \operatorname{MSE}\left(y, y_{-}\right)=\frac{\sum_{k=0}^{n}(y-y)^{2}}{n} $$
用神经网络实现鸢尾花分类:梯度下降
目的:想找到一组参数w和b,使得损失函数最小。
梯度:函数对各参数求偏导后的向量。函数梯度下降方向是函数减小方向。
梯度下降法:沿损失函数梯度下降的方向,寻找损失函数的最小值,得到最优参数的方法。
学习率(learning rate, Ir) :当学习率设置的过小时,收敛过程将变得十分缓慢。而当学习率设置的过大时,梯度可能会在最小值附近来回震荡,甚至可能无法收敛。
右边的这个公式很重要!

用神经网络实现鸢尾花分类:反向传播

下面我们用上一节右图的公式来体会下反向传播。这里我们先不用损失函数那小节的均方误差损失函数,我们以下面单独的例子作为演示。

import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
# 超参数lr初始值:0.2 (可自改学习率 0.001 0.999 看收敛过程)
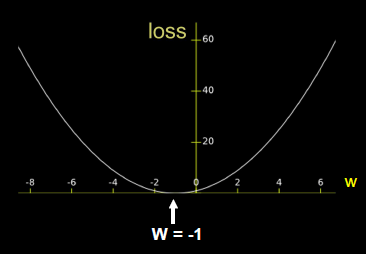
# 最终目的:找到 loss 最小 即 w = -1 的最优参数w
w = tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40
for i in range(epoch): # for epoch 定义顶层循环,表示对数据集循环epoch次,此例数据集数据仅有1个w,初始化时候constant赋值为5,循环40次迭代。
# 用with结构让损失函数loss对参数w求梯度
with tf.GradientTape() as tape: # with结构到grads框起了梯度的计算过程。
loss = tf.square(w + 1)
grads = tape.gradient(loss, w) # .gradient函数告知谁对谁求导,此处为loss函数对w求偏导
w.assign_sub(lr * grads) # .assign_sub 对变量做自减 即:w -= lr*grads 即 w = w - lr*grads
print("轮数 %s epoch, w的值 %f, loss值(损失值): %f" % (i, w.numpy(), loss))
我们找到了w的最优值,即 w = -1。
张量生成
阶就是张量的维数。关于维数的概念之前的机器学习笔记中有涉及。回顾 –> 维度是什么?数据降维方法,降维的用途
张量(Tensor) :多维数组(列表)
阶:张量的维数
| 维数 | 阶 | 名字 | 例子 |
|---|---|---|---|
| 0-D | 0 | 标量 scalar | s=1 2 3 |
| 1-D | 1 | 向量 vector | v=[1, 2, 3] |
| 2-D | 2 | 矩阵 matrix | m=[[1,2,3],[4,5,6][7,8,9]] |
| N-D | N | 张量 tensor | t=[[[ 有几个中括号就是几阶张量 |
张量可以表示0阶到n阶数组(列表)
数据类型
tf.int,tf.floattf.int 32,tf.float 32,tf.float 64
tf.booltf.constant([True, False])
tf.stringtf.constant("Hello, world!")
如何创建一个Tensor
创建一个张量
tf.constant(张量内容, dtype=数据类型(可选))
代码示例
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
a = tf.constant([1, 5], dtype=tf.int64) # 本机默认 tf.int32 可去掉dtype试一下 查看默认的数据类型
print("输出张量a的所有信息:", a)
print("a的dtype:", a.dtype)
print("a的shape:", a.shape)
运行结果

将numpy的数据类型转换为Tensor数据类型tf. convert to_tensor(数据名,dtype=数据类型(可选))
代码示例
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
import numpy as np
a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype=tf.int64)
print("a:", a) # numpy格式
print("b:", b) # tf格式
运行结果

- 创建全为0的张量
tf. zeros(维度)
- 创建全为1的张量
tf. ones(维度)
- 创建全为指定值的张量
tf. fil(维度,指定值)
维度:
- 一维直接写个数
- 二维用[行,列]
- 多维用[n,m,.K….]
代码示例:
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
a = tf.zeros([2, 3])
b = tf.ones(4)
c = tf.fill([2, 2], 9)
print("a:", a)
print("b:", b)
print("c:", c)
运行结果

- 生成正态分布的随机数,默认均值为0,标准差为1
tf. random.normal (维度,mean=均值,stddev=标准差)
- 生成截断式正态分布的随机数
tf. random.truncated_normal (维度,mean=均值,stddev=标准差)
在tf.truncated_normal中如果随机生成数据的取值在(μ-2σ, μ+2σ) 之外,则重新进行生成,保证了生成值在均值附近。(μ:均值,σ:标准差)
标准差计算公式: $$ \sigma=\sqrt{\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}{n}} $$ 代码示例:
import tensorflow as tf
# 生成正态分布的随机数,默认参数均值是0,标准差是1。
d = tf.random.normal([2, 2], mean=0.5, stddev=1)
print("d:", d)
# 生成截断式正态分布的随机数
e = tf.random.truncated_normal([2, 2], mean=0.5, stddev=1)
print("e:", e)
运行结果

生成均匀分布随机数( minval, maxval ) tf. random. uniform(维度,minval=最小值,maxval=最大值)
代码示例
import tensorflow as tf
# 生成均匀分布随机数
f = tf.random.uniform([2, 2], minval=0, maxval=1)
print("f:", f)
运行结果
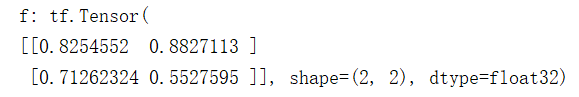
TensorFlow2常用函数
- 强制tensor转换为该数据类型
tf.cast (张量名,dtype=数据类型)
- 计算张量维度上元素的最小值
tf.reduce_ min (张量名)
- 计算张量维度上元素的最大值
tf.reduce_ max(张量名)
- 将tensor转换为numpy
tensor.numpy()
代码示例:
import tensorflow as tf
x1 = tf.constant([1., 2., 3.], dtype=tf.float64)
print("x1:", x1)
x2 = tf.cast(x1, tf.int32) # 强制tensor转换为该数据类型
print("x2", x2)
print("minimum of x2:", tf.reduce_min(x2)) # 计算张量维度上元素的最小值
print("maxmum of x2:", tf.reduce_max(x2)) # 计算张量维度上元素的最大值
a = tf.constant(5, dtype=tf.int64)
print("tensor a:", a)
print("numpy a:", a.numpy())
运行结果:

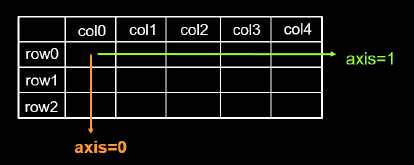
理解axis
在一个二维张量或数组中,可以通过调整axis等于0或1控制执行维度。axis=0代表跨行(经度,down),而axis=1代表跨列(纬度,across)。如果不指定axis,则所有元素参与计算。
- 计算张量沿着指定维度的平均值
tf.reduce_mean (张量名,axis=操作轴)
- 计算张量沿着指定维度的和
tf.reduce_sum (张量名,axis=操作轴)
代码示例
import tensorflow as tf
x = tf.constant([[1, 2, 3], [2, 2, 3]])
print("x:", x)
print("mean of x:", tf.reduce_mean(x)) # 求x中所有数的均值
print("sum of x:", tf.reduce_sum(x, axis=1)) # 求每一行的和
运行结果

变量tf.Variable
tf.Variable () 将变量标记为“可训练”,被标记的变量会在反向传播中记录梯度信息。神经网络训练中,常用该函数标记待训练参数。
tf.Variable(初始值)
神经网络初始化参数w的代码:
w = tf.Variable(tf.random.norma([2, 2], mean=0, stddev=1))
tf.random.norma([2, 2] 可以生成服从正态分布的随机数。后面就可以用梯度下降更新参数。
TensorFlow中的数学运算
- 对应元素的四则运算:
tf.add,tf.subtract,tf.multiply,tf.divide - 平方、次方与开方:
tf.square,tf.pow,tf.sqrt - 矩阵乘:
tf.matmul
对应元素的四则运算
- 实现两个张量的对应元素相加
tf.add (张量1,张量2)
- 实现两个张量的对应元素相减
tf.subtract (张量1,张量2)
- 实现两个张量的对应元素相乘
tf.multiply (张量1,张量2)
- 实现两个张量的对应元素相除
tf.divide (张量1,张量2)
注意:只有维度相同的张量才可以做四则运算
代码示例:
import tensorflow as tf
a = tf.ones([1, 3])
b = tf.fill([1, 3], 3.)
print("a:", a)
print("b:", b)
print("a+b:", tf.add(a, b))
print("a-b:", tf.subtract(a, b))
print("a*b:", tf.multiply(a, b))
print("b/a:", tf.divide(b, a))
运行结果

平方、次方与开方
- 计算某个张量的平方
tf.square (张量名)
- 计算某个张量的n次方
tf.pow (张量名,n次方数)
- 计算某个张量的开方
tf.sqrt (张量名)
代码示例:
import tensorflow as tf
a = tf.fill([1, 2], 3.)
print("a:", a)
print("a的平方:", tf.pow(a, 3))
print("a的平方:", tf.square(a))
print("a的开方:", tf.sqrt(a))
运行结果:

矩阵乘
实现两个矩阵的相乘
tf.matmul(矩阵1,矩阵2)
代码示例:
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
a = tf.ones([3, 2])
b = tf.fill([2, 3], 3.)
print("a:", a)
print("b:", b)
print("a*b:", tf.matmul(a, b))
运行结果:

传入特征与标签
神经网络训练模型的时候是把特征和标签配对喂入网络的。所以需要切分。切分传入张量的第一维度, 生成输入特征标签对,构建数据集
特征标签配对函数:data = tf.data.Dataset.from_tensor_slices((输入特征,标签))(Numpy和Tensor格式都可用该语句读入数据)
代码示例:
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
features = tf.constant([12, 23, 10, 17])
labels = tf.constant([0, 1, 1, 0])
dataset = tf.data.Dataset.from_tensor_slices((features, labels))
for element in dataset:
print(element)
运行结果

函数对指定参数求导gradient
with结构记录计算过程,gradient求 出张量的梯度
with tf.GradientTape() as tape:
若千个计算过程
grad=tape.gradient(函数,对谁求导)
代码示例,对函数x^2求x的导数 $$ \frac{\partial w^{2}}{\partial w}=2 w=2^{*} 3.0=6.0 $$
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
with tf.GradientTape() as tape:
x = tf.Variable(tf.constant(3.0))
y = tf.pow(x, 2)
grad = tape.gradient(y, x)
print(grad)
运行结果
枚举元素enumerate
enumerate是python的内建函数,它可遍历每个元素(如列表、元组或字符串),
组合为:索引元素,常在for循环中使用。
enumerate(列表名)
代码示例:
seq = ['one', 'two', 'three']
for i, element in enumerate(seq):
print(i, element)
运行结果:
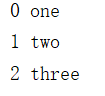
独热编码
独热编码(Cone-hot encoding) :在分类问题中,常用独热码做标签,标记类别: 1表示是,0表示非。
标签为1的独热编码为:
| 0狗尾草鸢尾 | 1杂色鸢尾 | 2弗吉尼亚鸢尾 |
|---|---|---|
| 0 | 1 | 0 |
tf.one_ hot()函数将待转换数据,转换为one-hot形式的数据输出。
tf.one_ hot (待转换数据,depth=几分类)
代码示例:
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
classes = 3
labels = tf.constant([1, 0, 2]) # 输入的元素值最小为0,最大为2
output = tf.one_hot(labels, depth=classes)
print("result of labels1:", output)
print("\n")
运行结果

使输出符合概率分布(归一化)
tf.nn.softmax(x)把一个N*1的向量归一化为(0,1)之间的值,由于其中采用指数运算,使得向量中数值较大的量特征更加明显。 $$ \operatorname{Softmax}\left(y_{i}\right)=\frac{e^{y_{i}}}{\sum_{j=0}^{n} e^{y_{i}}} $$ tf.nn.softmax(x)使输出符合概率分布
当n分类的n个输出(yo, y1…… yn_1)通过softmax( )函数,便符合概率分布,所有的值和为1。 $$ \forall x P(X=x) \in[0,1] \text { 且 } \sum_{x} P(X=x)=1 $$
以上结果表明,符合第0号标签的概率是25.6%;1号标签的概率是69.5%;2号标签的概率是4.8%。
代码示例:
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
y = tf.constant([1.01, 2.01, -0.66])
y_pro = tf.nn.softmax(y)
print("After softmax, y_pro is:", y_pro) # y_pro 符合概率分布
print("The sum of y_pro:", tf.reduce_sum(y_pro)) # 通过softmax后,所有概率加起来和为1
运行结果:

参数自更新
赋值操作,更新参数的值并返回。
调用assign_ sub前,先用tf.Variable定义变量w为可训练(可自更新)。
w.assign_ sub (w要自减的内容)
代码示例:
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import tensorflow as tf
x = tf.Variable(4)
x.assign_sub(1)
print("x:", x) # 4-1=3
运行结果
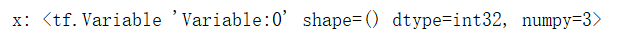
指定维度最大值索引
返回张量沿指定维度最大值的索引
tf.argmax (张量名,axis=操作轴)
代码示例:
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 关闭log信息
import numpy as np
import tensorflow as tf
test = np.array([[1, 2, 3], [2, 3, 4], [5, 4, 3], [8, 7, 2]])
print("test:\n", test)
print("每一列的最大值的索引:", tf.argmax(test, axis=0)) # 返回每一列最大值的索引
print("每一行的最大值的索引", tf.argmax(test, axis=1)) # 返回每一行最大值的索引
运行结果:

鸢尾花数据集读入
数据集介绍
共有数据150组,每组包括花尊长、花尊宽、花瓣长、花瓣宽4个输入特征。同时给出了,这组特征对应的鸢尾花 类别。类别包括Setosa Iris (狗尾草鸢尾),Versicolour lris (杂色鸢尾),Virginica Iris (弗吉尼亚鸢尾)三类,分别用数字0,1,2表示。
读取数据集代码
from sklearn import datasets
from pandas import DataFrame
import pandas as pd
x_data = datasets.load_iris().data # .data返回iris数据集所有输入特征
y_data = datasets.load_iris().target # .target返回iris数据集所有标签
print("x_data from datasets: \n", x_data)
print("y_data from datasets: \n", y_data)
x_data = DataFrame(x_data, columns=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度']) # 为表格增加行索引(左侧)和列标签(上方)
pd.set_option('display.unicode.east_asian_width', True) # 设置列名对齐
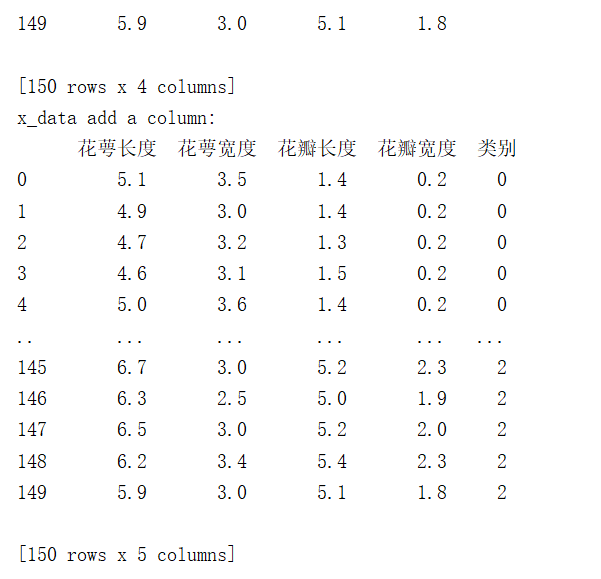
print("x_data add index: \n", x_data)
x_data['类别'] = y_data # 新加一列,列标签为‘类别’,数据为y_data
print("x_data add a column: \n", x_data)
#类型维度不确定时,建议用print函数打印出来确认效果
神经网络实现鸢尾花分类
- 准备数据
- 数据集读入
- 数据集乱序
- 生成训练集和测试集(即x_ train/y train, x_ test/y_ test)
- 配成(输入特征,标签)对,每次读入一小撮(batch)
- 搭建网络
- 定义神经网路中所有可训练参数
- 参数优化
- 嵌套循环迭代,with结构更新参数,显示当前loss
- 测试效果
- 计算当前参数前向传播后的准确率,显示当前acc
- acc / loss可视化
代码示例:
# -*- coding: UTF-8 -*-
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
"""
数据集读入
"""
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
"""
数据集乱序
"""
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
"""
数据集分出永不相见的训练集和测试集
"""
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
"""
配成[输入特征, 标签]对,每次喂入一小撮(batch)
"""
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
"""
定义神经网络中所有可训练的参数
"""
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
"""
嵌套循环迭代,with结构更新参数,显示当前loss
"""
# 训练部分
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all/4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
"""
计算当前参数前向传播后的准确率
"""
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
"""
acc/loss可视化
"""
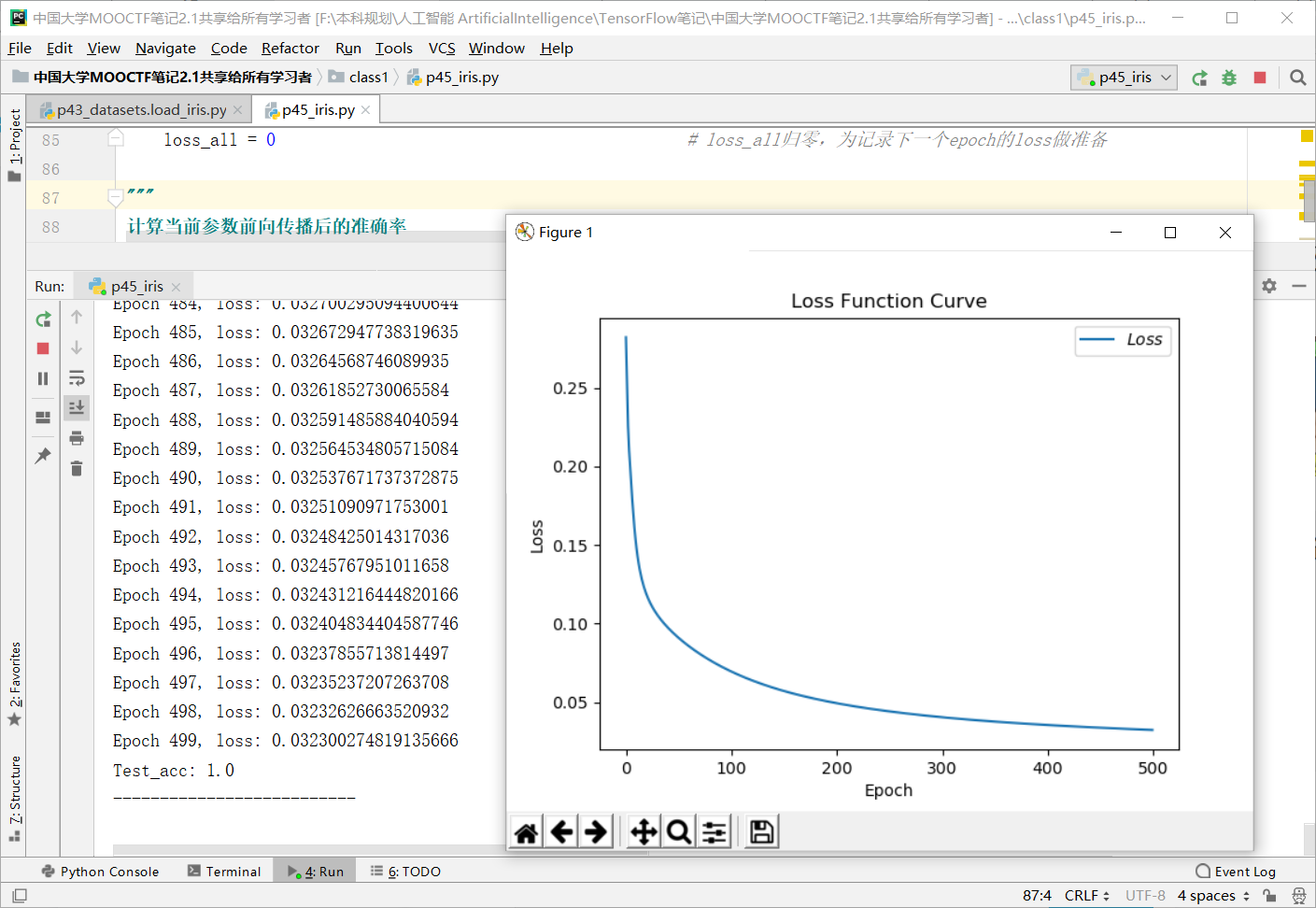
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
 参考资料:
https://www.bilibili.com/video/BV1Cg4y1q7Xq
https://github.com/dxc19951001/Study_TF2.0/blob/master/tensorflow2.md
参考资料:
https://www.bilibili.com/video/BV1Cg4y1q7Xq
https://github.com/dxc19951001/Study_TF2.0/blob/master/tensorflow2.md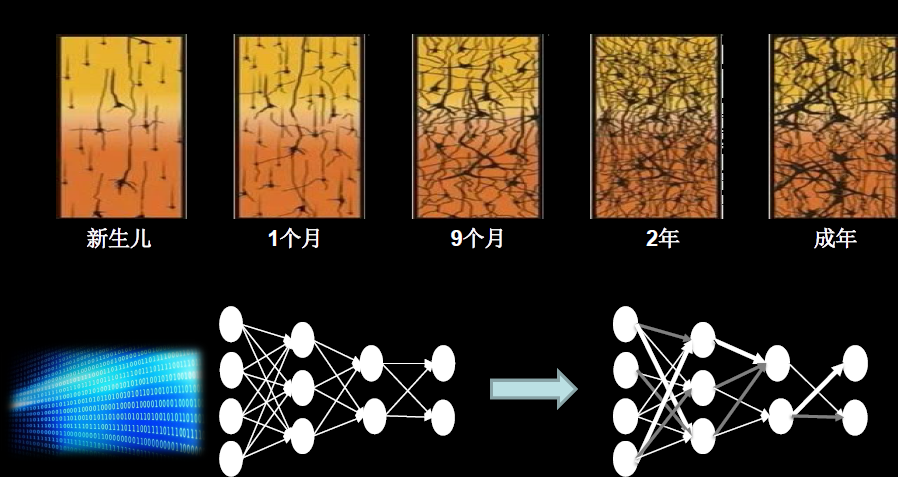
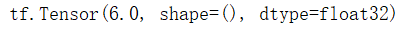

你好,鸢尾花分类这里的代码似乎有误
感谢反馈,具体是哪一段代码呢
epoch包含验证集和测试集的循环。在页面的代码,测试集的循环没在epoch循环里面
epoch包含验证集和测试集的循环。在页面的代码,测试集的循环没在epoch循环里面