[title]拉格朗日乘子法要解决什么问题[/title]
我们以二维空间为例,简单介绍下拉格朗日乘子法解决的问题。
解决的问题:在$h(x)=x_{1}^2+x_{2}^2-2=0$函数的约束下(即上图红色的圆柱)上找到某一点使得f(x)函数(蓝色平面)值取得最小值。我们称h(x)为限制条件。

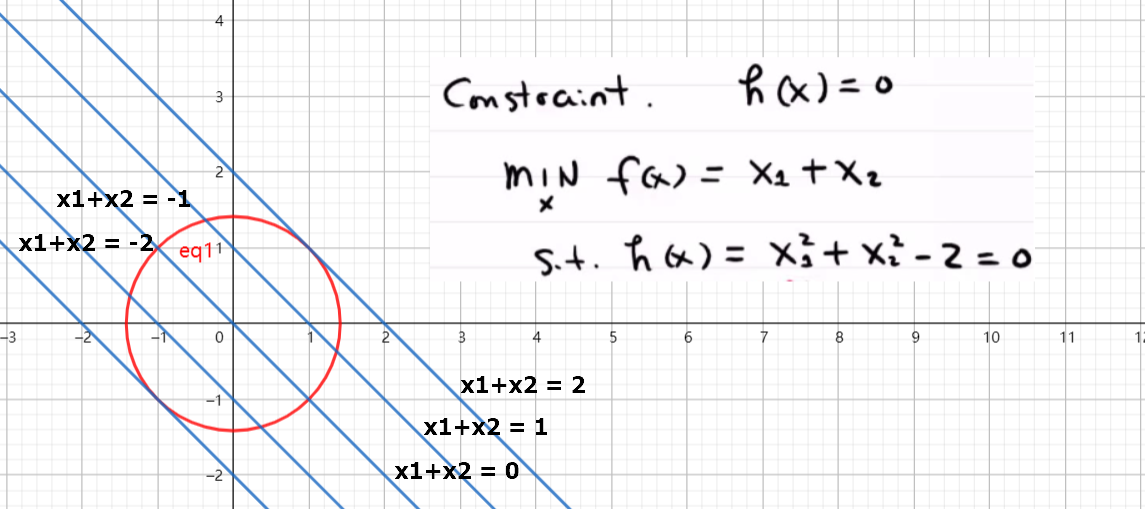
[title]如何在约束函数的条件下找到极值点(即确定优化的最终点)?[/title]
如何找到梯度向量?
f(x)梯度向量
对$f(x)=x_{1}+x_{2}$,
$\frac{f(x)}{\partial x_{1} } = 1$
$\frac{f(x)}{\partial x_{2} } = 1$
$\nabla _{x}f(x) = \begin{pmatrix}
1\\1
\end{pmatrix}$
h(x)梯度向量
$h(x) = x_{1}^2+x_{2}^2-2$函数是下图的红色圆。
如何一步步的逼近这个极值点?
使用梯度下降法找到梯度向量,简单的来说就是对二元函数h(x)求他的偏导数。得到h(x)的梯度向量。关于梯度下降的算法可以参考:梯度上升法通俗的理解 – 以一个一元二次函数为例
点A(1, 1)的梯度向量为$\binom{2x_{1}}{2x_{2}} =\binom{2\times {}1}{2\times 2 } = \binom{2}{2} $。
点B(1, -1)的梯度向量为$\binom{2x_{1}}{2x_{2}} =\binom{2\times {}1}{2\times -2 } = \binom{2}{-2} $。
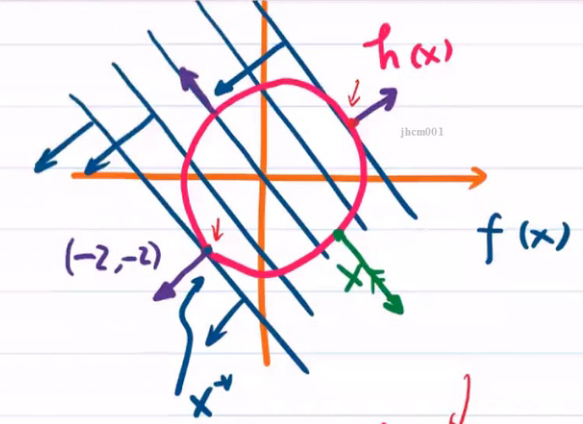
我们画出的四个点A、B、C、D的梯度向量。最终发现梯度的方向总是垂直于图形的。其实梯度的方向也总是垂直于等高线的。
这也意味着,如果两条曲线相切,意味着他们在这个点上,两者的梯度一定是平行的。
———————————————–
结论:在极值点,f(x)与h(x)一定相切,且当f(x)函数和约束函数h(x)的梯度平行时,即有可能为优化问题的终止点,但不是所有的相切点都是极值点。
[title]引出拉格朗日乘子法[/title]
在极值点的特性,梯度向量平行:$\nabla f(x) = \lambda \nabla g(x)$
同时需要有约束条件$h(x) = x_{1}^2+x_{2}^2-2$,联立方程:
$\begin{cases}
\nabla f(x) = \lambda \nabla h(x)
\\
h(x) = x_{1}^2+x_{2}^2-2
\end{cases}$
定义:
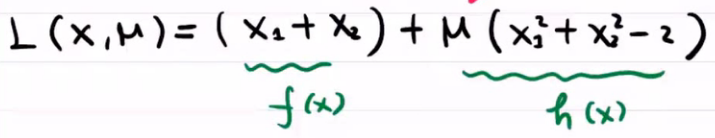

接下来我们得到最优点x和$\mu $
参考文献:
https://www.zhihu.com/question/38586401
https://www.bilibili.com/video/BV1h4411v7VY?p=10