本文已收录到:中科大编译原理学习笔记 专题
语法分析的目标
语法分析的最终目标是生成抽象语法树。


上下文无关文法:用数学理论描述语言的语法规则
早有数学家帮我们构造好了数学方法,数学的发展总是快工程一步!
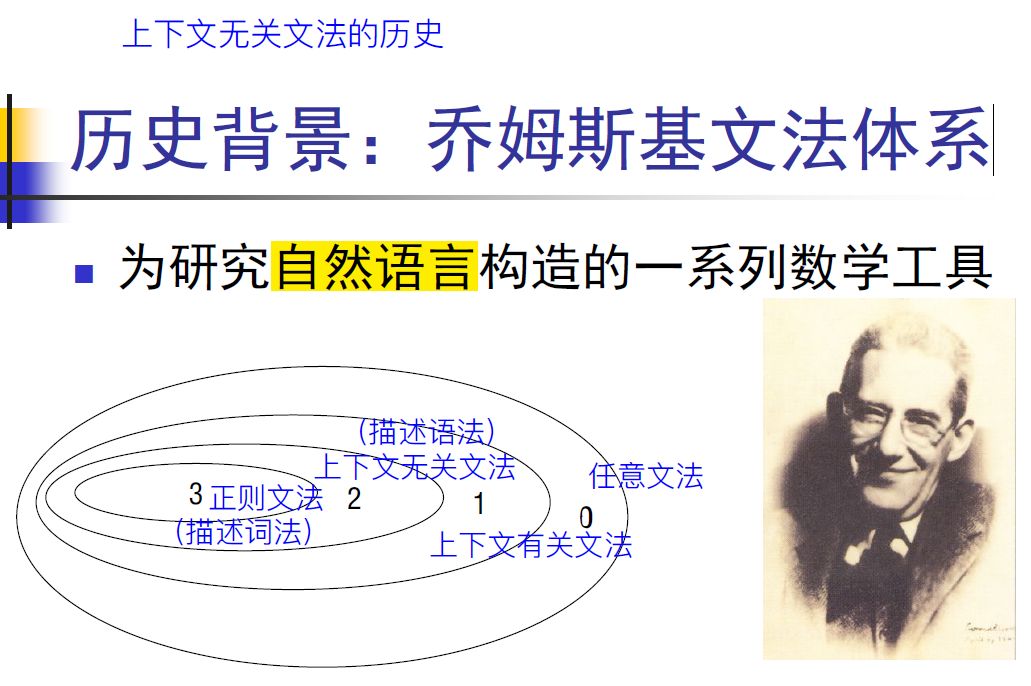
3型文法描述语言的词法结构;2型文法描述语言的语法结构。上图的文氏图表示更外部的文法描述的范围更广。1型文法和0型文法在目前的程序语言中还没有得到广泛应用。
小学的造句练习:

对现象可以抽象画总结归纳:

- -> 代表推导
- | 代表或
如果是程序语言:

问:如何区分终结符和非终结符?
答:人为规定,大写的是非终结符,小写的字母是终结符,并且E永远是起始符。
Ps:这里用到的规则可能跟文献上不大一样,文献上用的叫BNF范式,也叫巴克斯淖尔范式。
巴克斯淖尔范式的写法规则是:非终结符要放在尖括号里,终结符要加下划线。下图这样:

推导

S -> NVN :因为开始符号S的产生式右部只有一种情况 NVN,所以直接将S替换成 NVN。
后面,NVN可以替换任意一个非终结符,这里替换中间的V。
最终得到的,没有非终结符的串称为句子。
一共会有多少种不同的句子?排列组合去算

推导可以分为最左推导和最右推导。
语法分析器的任务:
![]()

分析树与二义性
对于上面的推导,可以改造成树的形式,叫做分析树。


3+4*5 表达式的例子(最左推导):

问:第一个推导是怎么知道选 E+E 的,而不是其他?
答:选其他的也可以,但为了匹配我们想推导的句子。后面再讨论如何正确的选择推导的右部问题。
如果采取最右推导:

会出现优先级问题,他们推导出来的分析树是不同的。

分析树的含义取决于后序遍历。关于树的遍历可以参考 [LeetCode] 145. 二叉树的后序遍历 (Binary Tree Postorder Traversal)
二义性文法
给定一个文法G,如果存在句子s,它有两棵不同的分析书,那么称他为二义性文法。
解决方案:文法的改造。
表达式文法的重写
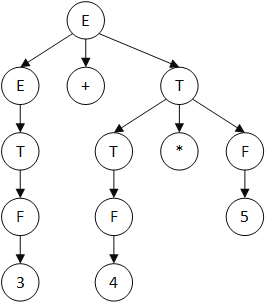
下面是对算术表达式 3+4*5 进行文法的重写,还是最左推导:
E -> E + T
| T
T -> T * F
| F
F -> num
| id
推导出句子 3 + 4 * 5 的过程如下:
E -> E + T -> T + T -> F + T -> 3 + T -> 3 + T * F -> 3 + F * F -> 3 + 4 * F -> 3 + 4 * 5写成分析树的形式:
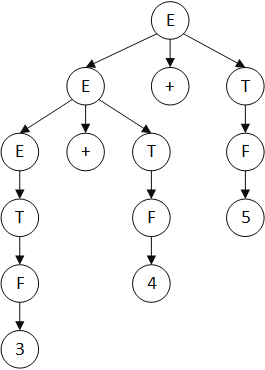
若推导出的句子是 3 + 4 +5, 则推导过程如下:
E -> E + T -> E + T + T -> T + T + T -> F + T + T -> 3 + T + T -> 3 + F + T -> 3 + 4 + T -> 3 + 4 + F -> 3 + 4 + 5
特点:树越往下优先级越高;因为改进的文法是左递归的,所以保证了加法的左结合性,同样的如果改写为右递归就能变成右结合性。