作为《数据结构》课程第一章绪论的内容,时间复杂度的算法也是本书最基础的内容。因为《数据结构》这门课(严格来说应该叫《数据结构与算法》),主要就是在研究程序的执行效率。尽可能的使写的程序在性能同样的机器上运行会更快。
作为基础内容,也是考研的必考题。时间复杂度的算法需要有一定的初等数学(即中学数学)基础和简单的数列知识。
数学基础
基本初等函数
我们只用记得它们的函数图像和走势即可,并且仅研究定义域>0的情况。
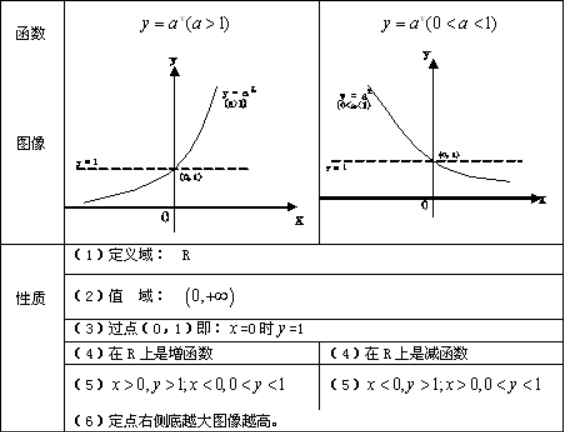
指数函数:
一般地,y=ax函数(a为常数且以a>0,a≠1)叫做指数函数。函数图像如图:
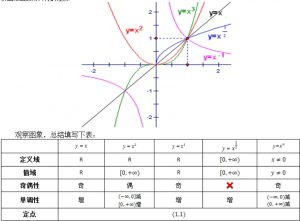
幂函数
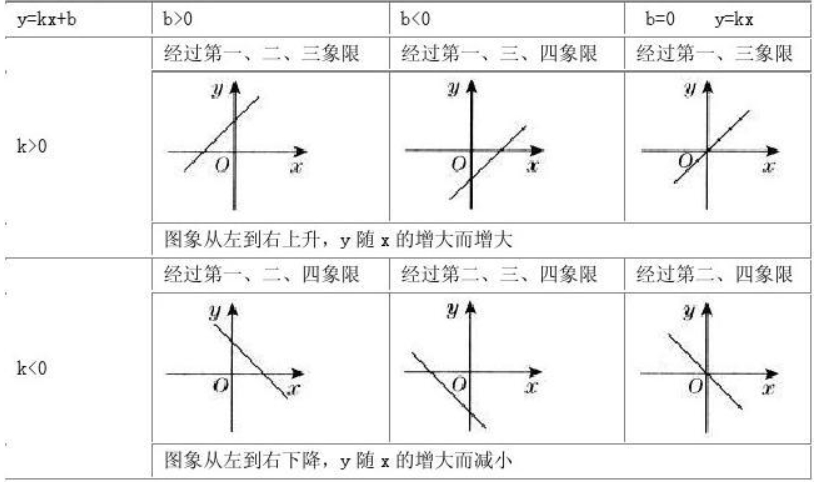
一次函数
对数函数
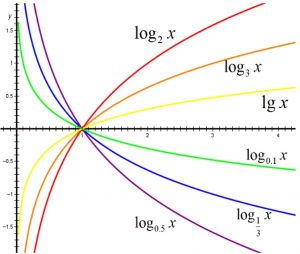
我们学习时间复杂度的算法,以及各种复杂度的函数变化无非就是以上几种。全部都是高中所学过的基本初等函数。希望你能够回想起来,然后在脑子里有他们的大概变化曲线。知道哪个函数随着x的值增大变化较慢,而哪个函数会很快。
如果以上的函数基础你都没有问题,那么下面的基本代数计算就更简单了。这是小学和初中所学过的。
简单代数计算
数数
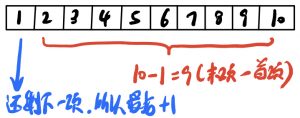
问:从1(含)~10(含)共有几项?
答:有“1”、“2”、“3”、“4”、“5”、“6”、“7”、“8”、“9”、“10”。用手指数一下,共有10项。
计算方法:项数=末项-首项+1
指数与对数互换
问:2t=n,t=?
答:t=log2n
若aⁿ=b(a>0,且a≠1),称为a的n次幂等于b。在这里,a叫作底数,n叫作指数,
b是以a为底的n次幂。
若写成对数形式就是:
在这里,a仍然叫作底数,b叫作真数,而n叫作以a为底b的对数。
由此可见,指数和对数都是n,即它们是指同一个东西,只是在不同场合叫不同的名字。
OK,数学所需的基础也就这些。普遍都是我们已经很熟悉的东西。
算法执行次数T(n)
我们通常用T(n)表示算法执行了多少次。其中n代表问题规模。
典例一:单层循环
例如下面的程序:
#include <stdio.h>
int main(void) {
for (int i = 0; i<n; i++) { //执行了n+1次
printf("Hello World!"); //执行了n次
}
return 0;
}
分析:
- 这个程序肯定是无法运行的(变量n未定义),所以我们不运行它。我们先分析循环里面的printf()语句:
- 根据上面的数学知识,“i从0(含)到n(不含)”等价于“i从0(含)到n-1(含)”——请停下来好好想下,没想通的话不要继续看下面的内容,请留言告诉我。
- 那么,i从0(含)到n-1(含)共执行了(n-1)-0+1=n次。所以最内层执行了n次。
- 因为“for (int i = 0; i<n; i++)”执行到最后,当i=n时,虽然不满足i<n的条件。但仍然算执行了一次。——认真想明白后再往后看,如果想不通,请试数(将n取5或任何数,数一数执行了多少次,很显然是6次)
典例二:双层嵌套“内外都不变”循环
我们再看一个程序:
#include <stdio.h>
int main(void) {
for (int i = 0; i<n; i++) {
for (int j = 0; j<n; j++) {
if (... ...) //共执行n*n次
}
}
return 0;
}
问:什么叫内外都不变?
答:观察程序,发现外层循环变量i是从0开始,并且不会自增或自减。同样的,内层循环变量j也是从0开始,不会自增或自减。笔者自己定义,把这样的嵌套循环叫做双层嵌套“内外都不变”循环。
我们讨论程序执行次数的时候,会发现执行最多的往往是循环最内层的代码。所以我们以后在分析算法的执行次数时,就可以只考虑最内层的循环。因为它最有代表性。
那么,这个n的平方次是怎么计算出来的呢?
分析:
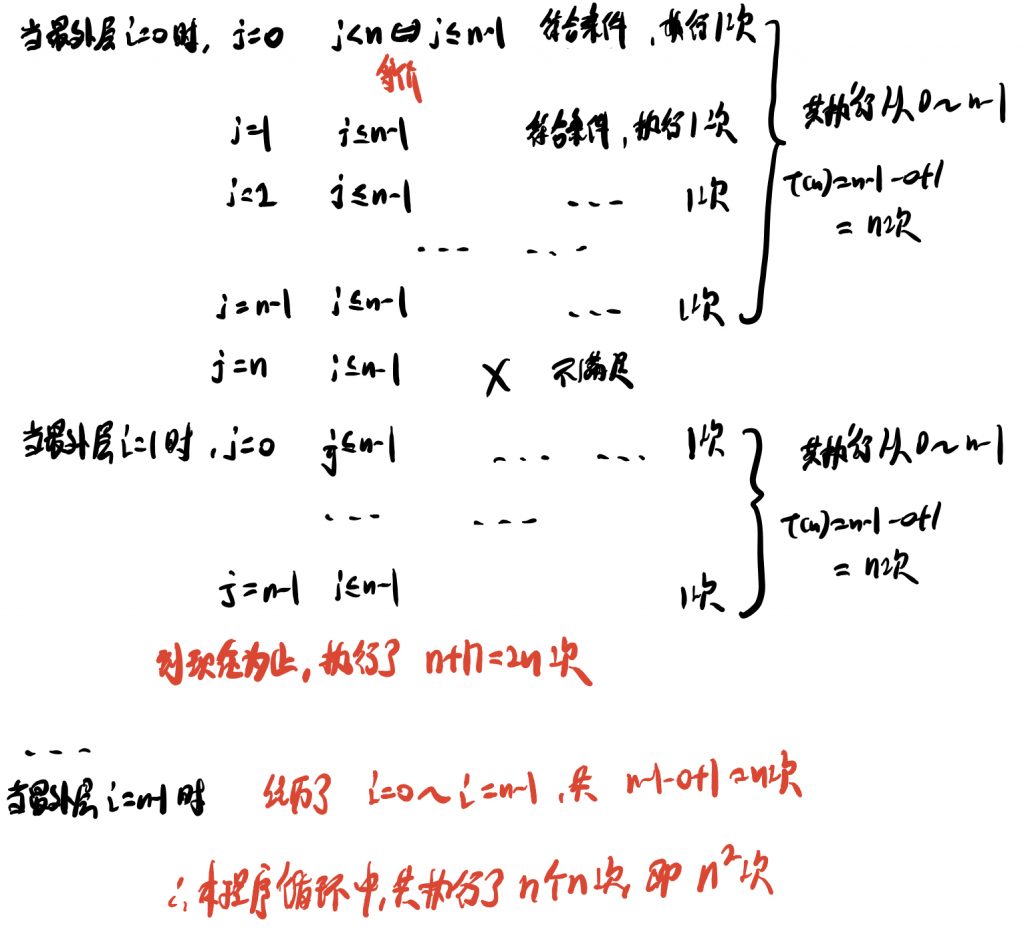
典例三:双层嵌套“内变外不变”循环
#include <stdio.h>
int main(void) {
for (int i = 0; i<n; i++) {
for (int j = i; j<n; j++) { //内层j会随着i的改变而自增
... ....
}
}
return 0;
}
分析:

典例四:循环变量非连续增加或减少式
#include <stdio.h>
int main(void) {
int i=0;
while (i<n) {
i=i+2;
}
return 0;
}
分析:
注意观察变量i不再是像前面那样每次增加i(自增)了。而是自增2。
其实,我们主要还是要找到执行次数、自增变量和临界问题规模n的数学关系式。并用t=?的形式表达出来。
易错:(这个解法存在问题!)
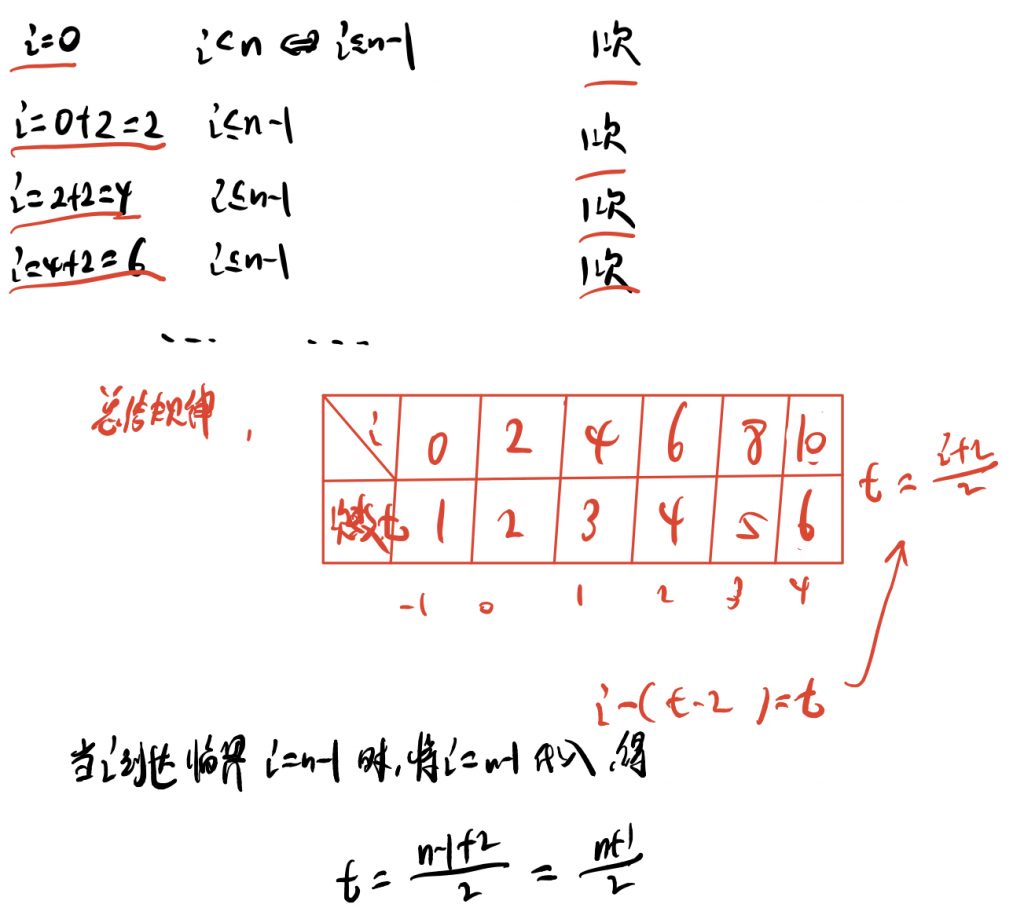
这个解法看的一瞬间感觉不到什么问题,但问题在于i=0时,是否计算在第一次中?
很显然,我们观察程序发现。i=o这条具体在循环体外部,而执行第一次的时候,i=0+2是等于2的。
所以i=0时,不计算在第一次中!本解法错误!
正确解法:
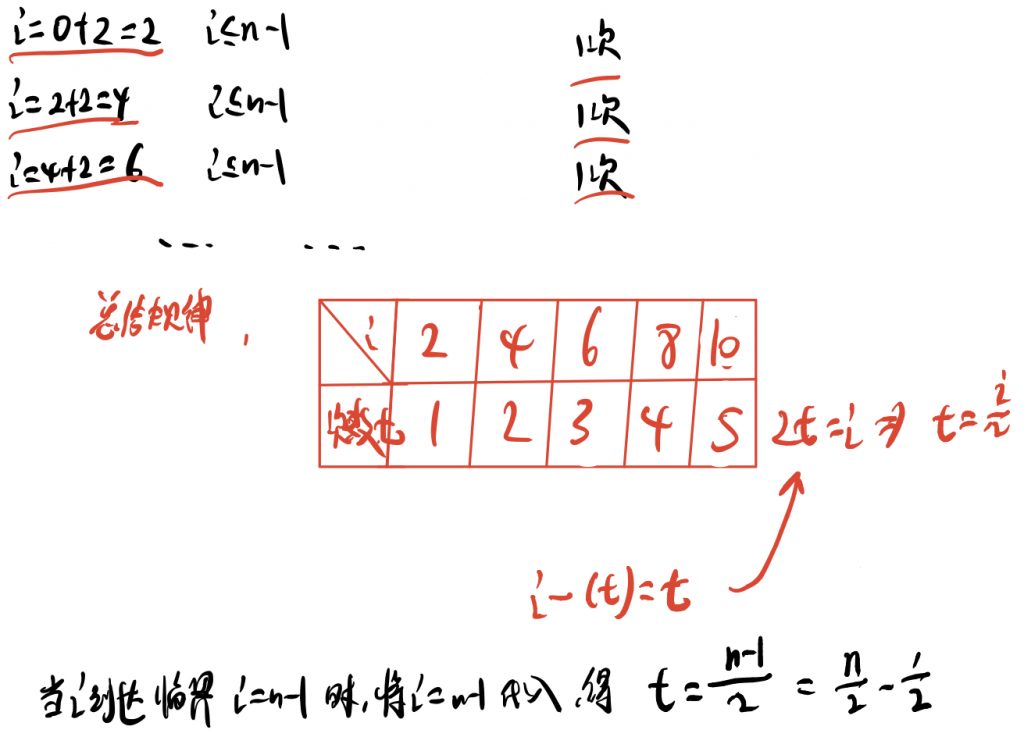
典例五:循环变量指数增加式
#include <stdio.h>
int main(void) {
int i=0;
while (i<n) {
i=i*2;
}
return 0;
}
易错:注意观察i的初值式0,意味着i=i*2这个语句不管执行多少次,i的值都会是0。所以这个程序无论如何都达不到临界问题规模n。我们成为死循环。
#include <stdio.h>
int main(void) {
int i=1;
while (i<n) {
i=i*2;
}
return 0;
}
分析:

典例六:顺序执行的语句或者算法
#include <stdio.h>
int main(void) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
printf("Hello, World!\n"); //执行次数为n^2次
}
}
for(int j = 0; j < n; j++) {
printf("Hello, World!\n"); //执行次数为n次
}
return 0;
}
两部分循环的次数,跟前面一样,你应该都会计算了。他们分别是n2和n次。
那么一共执行多少次呢?应该是n2+n次。
典例七:含有条件判断语句式
#include <stdio.h>
int main(void) {
if (...) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
printf("Hello, World!\n"); //执行次数为n^2次
}
}
} else {
for(int j = 0; j < n; j++) {
printf("Hello, World!\n"); //执行次数为n次
}
}
return 0;
}
很显然,有if组成的程序语句,只能只能其中的某一个语句。这是有题目本身的条件所决定的。
所以本程序要么执行n2次,或者执行n次。这是不确定的。
函数的渐近增长
回到最初我们的目的。《数据结构与算法》是以研究程序执行速度为根本的。
前面我们所计算的程序执行次数,有n(n+1)/2次、有(n+1)/2次、(n-1)/2次,还有log2(n-1)次。
这些全都是基本初等函数的简单变形。我们把他们与函数图像进行对照:
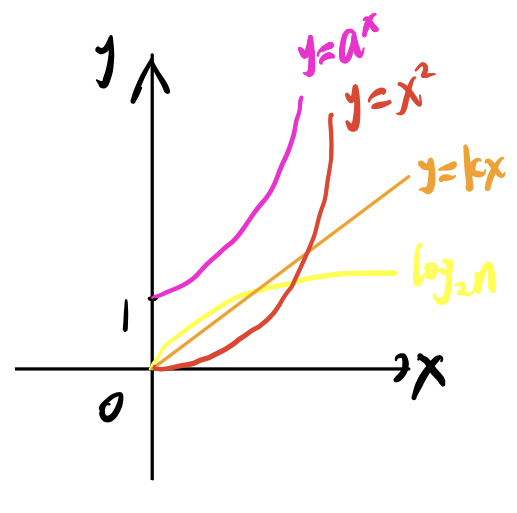
根据图像,我们可以总结出函数变化速率为:
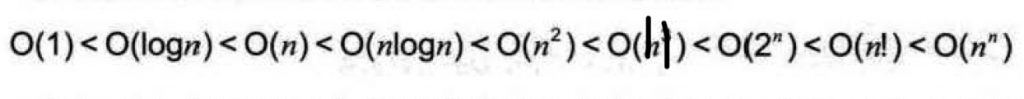
在相同的问题规模n下,我们应该选择执行次数函数变化小的算法。这样会使程序在相同的硬件平台下运行的更快。
算法时间复杂度
问题还没有结束,虽然我们知道了执行次数函数的意义。但是,它与初等函数并不完全一样。
我们需要讨论哪些量是可以被忽略的,从而是执行次数函数更像基本初等函数。
加减法常数
(n+1)/2、(n-1)/2、n/2对比:

无论是+1还是-1,对函数的变化趋势无影响。
所以我们认为:可以忽略掉加减法常数。
项后面的常数
同样的,对比算法A和算法C、算法B和算法D。
忽略项后面的常数项。对整个函数的变化趋势无影响。
与n相乘的常数

数量级还是一样的,不影响变化趋势。
我们还可以大胆的忽略掉与高阶n相乘的数。
总结:
- 我们基本可以分析出:随着问题规模n的增长,某一算法可能越来越优于某种算法,也可能越来越差于某种算法。我们分析时间复杂度时只关心影响变化趋势最大的高阶数。
- 所以我们又把时间复杂度称为渐进时间复杂度。
- T(n)是执行次数函数、f(n)是问题规模的某个函数、O(n)是渐进时间复杂度。
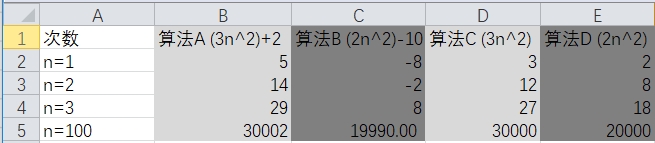
常见时间复杂度O(n):
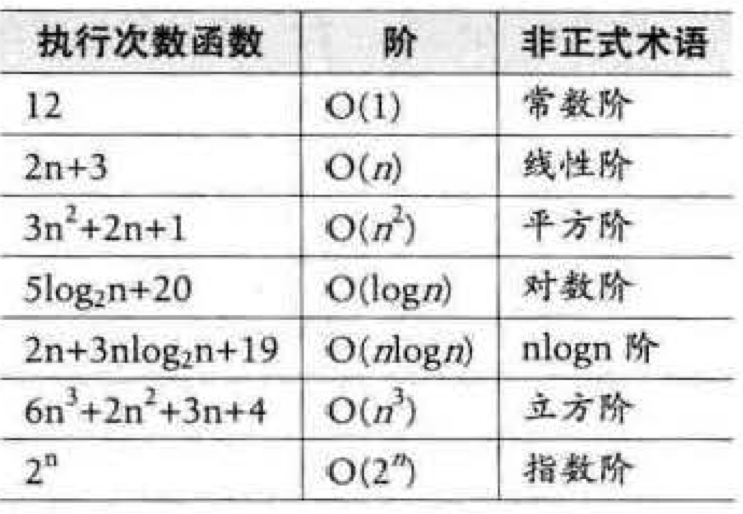
请自行分析上述7个典型例题的时间复杂度。
最坏情况与平均情况
如果我们需要在一个一维数组中查找某个数字,有两种极端情况:
情况一:它恰好在第一个位置,则时间复杂度为O(1)
情况二:不巧!在最后一个位置。时间复杂度是O(n)
这两种情况的时间复杂度相差很大。所以我们规定:
最坏时间复杂度:除非特别规定,否则我们提到的运行时间都是最坏情况下的运行时间。
平均时间复杂度:当然,平均运行时间O(n/2)是最有意义的,他是我们期望的运行时间。
一般,没有特殊说明的情况下,我们都是指最坏时间复杂度。