本文已收录到:CS143斯坦福编译原理学习笔记 专题
- CS143 斯坦福编译原理 Cool语言概述
- CS143 斯坦福编译原理 词法分析
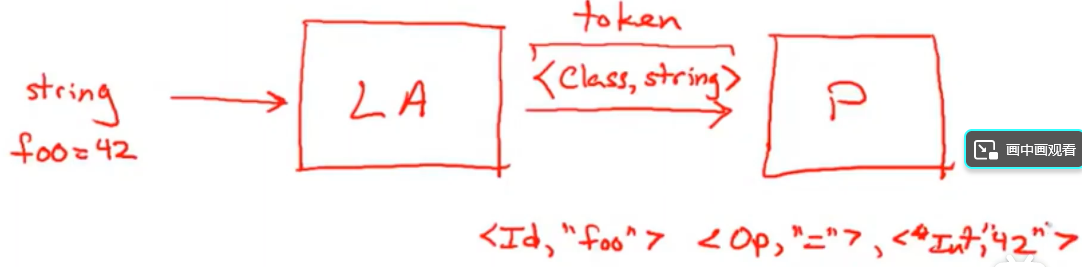
词法分析任务
任务:将代码分解成为<class, string>形式,这叫做Token(词法单元)。
Cool包括以下几个类别:
- 标识符(Identifier):指的是变量名、函数名或类名等名称。此外,+或-等运算符及括号等标点符号也属于标识符。标点符号与保留字有时也会被归为另种类型的单词,但这里不对他们区分,都作为标识符处理。以字母开头后续为若干个字母或数字的字符串。eg:A1、Foo、B17。Ps:标识符主要限制的就是以字母开头。
- 整型字面量(integer literal):数字字符串。eg:0、12
- 关键词(Keyword):eg:if,else、begin等
- 空格标记(Whitespace):空格字符、回车换行符、制表符。eg: 、\n、\t


eg:
为什么要往前看?

DO 5 i = 1, 25
解释:这种是FORTRAN语言的一种类似C语言for循环的语句,其中DO是关键词,5表示从这行开始往下5行都是本轮DO循环语句,i表示的是迭代变量,就类似C语言for循环中的i变量一样,1, 25表示的是i从1循环到25。翻译过来就像C语言的:
for (i=1, i<=25, i++)
{
第1行
第2行
... ...
第4行
第5行
}
下面这个与它很相似的代码:
DO 5 i = 1.25
仅仅是把逗号换成了小数点,意义就从循环语句变成了变量赋值语句,DO5i是一个变量的名字:
DO5i = 1, 25
出现这种问题说明了我们词法分析器在读取到1后面的逗号或者是小数点之前,是不知道前面的DO5i到底是什么的(代码中的所有空格都被视为无意义的,会被清除)。为了理解这里面的DO是循环语句的标识符还是变量名称的一部分,这就需要一种预先读取机制,或者说是“往前看”的机制来解决这个问题。
这样的话设计词法分析器就比较复杂了,但向前看又是必须的, ,这样做就会在相当程度上简化我们词法分析器的实现。
,这样做就会在相当程度上简化我们词法分析器的实现。
更多的向前看需求:

当词法分析器扫描到e的时候,不确定e是变量名称的一部分还是else中的e。所以还是需要向前看。
还有上面的 i == j的双等号,扫描一个等号后,究竟是赋值操作还是等号操作,需要向前看!
不保留关键词的编程语言会使得词法分析比较困难
PL1是一款由IBM公司开发的编程语言,他的一个典型的特点是不保留关键词的,这意味着你可以书写下图这样的代码:

如果不告诉你哪个是PL1的关键词,是不是代码看起来会非常头疼。所以我用蓝色的圈圈圈起来了我们的关键词。剩下的关键词ELSE等都是变量名。
这说明如果我们开发一款不区分关键词的编程语言的词法分析器,这就会变得很难!
再比如下面这样:
![]()
DECLARE是函数名还是数组名?——取决于后面有没有等号,如果有等号就是数组名,如果没有等号就是函数名。这个例子最有趣的是函数本身是不限制参数个数的,所以 … …你不得不扫描到右括号。
你可能会说这些都是上个世纪很古老的编程语言,那么大家现在都在用的新的编程语言有这样的问题吗?其实也是有的:
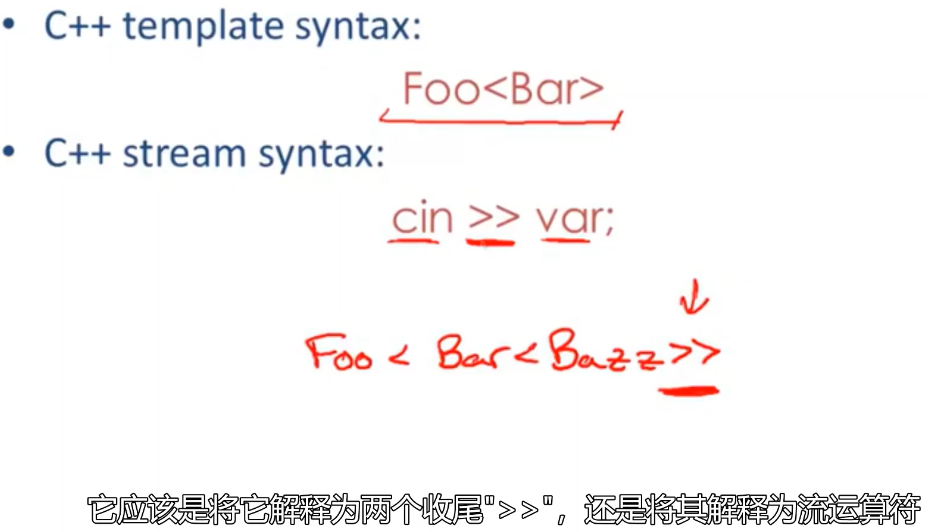
当然现在大多数的C++编译器解决了这个问题,他们通常会把 >> 解释为流运算符。
正则语言
正则表达式感觉讲的一般。可以单独学习。
形式语言
正则表达式是形式语言的一个例子,形式语言就是一套语法规则。例如一个电子邮箱应该长得是什么样子,什么样的字符串表示的是合法的电子邮箱的地址。在编程语言中语法规则就是一种形式语言。例如函数如何书写,变量声明和赋值方式。
词法分析器实现方法一:手工构造法
手工构造法

转移图

转移图算法

识别关键字
- 在原来状态转移图上扩展新的边
- 关键字表算法
- 对给定语言中所有的关键字,构造关键 字构成的哈希表H
- 对所有的标识符和关键字,先统一按标 识符的转移图进行识别
- 识别完成后,进一步查表H看是否是关键字
正则表达式


文法规则
文法规则就是一个编程语言
标识符(Identifier)、整型字面量(integer literal)、关键词(Keyword)等的规则。
贪婪匹配
例如“=”在编程语言中是赋值运算符,“==”是比较运算符。词法分析器会采取最长匹配。


这也符合日常常理,
同时满足多条语法规则
如果字符串同时满足两个语法规则,例如字符串if既是关键字又是标识符,如何处理?
大部分的编程语言对于if只认其实关键字,因为关键字被设定为保留的,不可能是标识符。优先度的选择也可以解决这个问题。
如果没有匹配上任何规则该怎么办?
对于编译器来说,做好错误处理是非常重要。需要能够给程序员报出错误的位置以及错误的类型。对于词法分析器来说是不期望有这样的事情的,对于处理来说,可以用一些正则表达式去匹配这些“不合规”的字符串并把它们的优先级置为最低。
词法分析器实现方法二:用工具(讲述原理)

有限状态自动机FA
五元组与FA
接收有限的字符串,输出YES或者NO。验证——某个自动机能否接收你输入的字符串。可以用五元组表示。

例子:

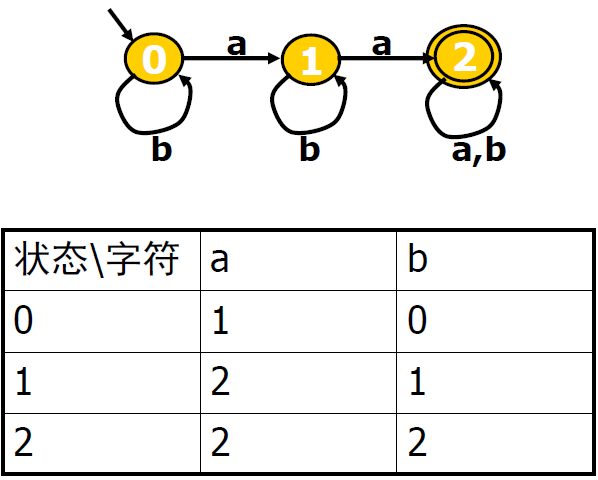
上述自动机的各项信息如下:
字母表 = {a, b}
状态集:0,1,2
起始状态:0号节结点有箭头
终结状态集:2号结点,有两个圈。Ps:有些自动机有多个终结状态。
转移函数: ,(q0, a)–>q1 表示q0读到字母a就可以转移到转态q2。
,(q0, a)–>q1 表示q0读到字母a就可以转移到转态q2。
RE->NFA
正则表达式与有限自动机密切相关,确切地说我们可以这么认为,它们都是同一种语言,即正则语言。
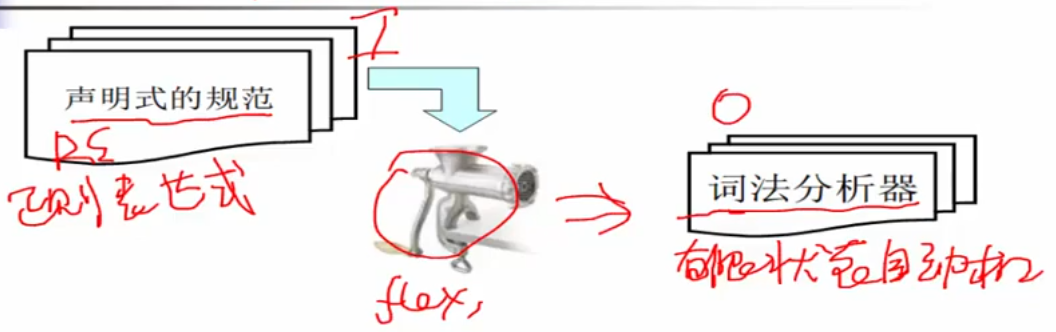

非确定有限状态自动机NFA
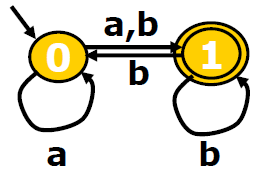
状态0读入一个字符串“a”后,可以回到0状态也可以跳转到1状态。如果是回到0状态就会被认为字符串不可别接受,如果跳到1状态就表示可被接收。这种状态显然是不确定的。——非确定有限状态自动机
在NFA上判断接收要遍历,一条路走不通还需要回溯,比较麻烦。我们后面会将其转换为等价的确定有限状态自动机DFA。

DFA的实现
在数据结构中,可以看成带有边和结点的有向图。
特点:
- 边上有信息。其实数据结构中也有边有信息的例子。
- 结点上有信息。
可用临界表,邻接矩阵表示。
RE -> NFA: Thompson算法
算法思想:

从RE到NFA:
直接构造,对空串和字符:
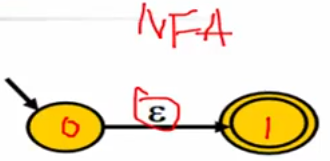
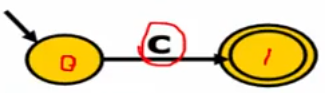
复合构造,递归构造
eg:
- 先构e1小自动机:

- 构造e2小自动机:

- 以上是小的自动机,然后通过 | 运算整合在一起构成大的自动机。——递归的思想。两个小的自动机整合需要去掉e1自动机终止状态和e2自动机的开始状态,整合后:

更多例子:
NFA->DFA
子集构造算法:工作表算法
使用子集构造算法可以帮助我们将NFA转换为DFA,因为NFA存在回溯。
算法思想:https://www.bilibili.com/video/BV1m7411d7iS?p=17
q0 <- eps_closure(n0) // q0 = {n0}
Q <- {q0} // Q = {q0}
workList <- q0 // workList = [q0, ...]
while(workList != [])
remove q from workList // workList = [...]
foreach(character c) // c = a
t <- e-closure(delta(q,c)) // delta(q0, a) = {n1}, t = {n1, n2, n3, n4, n6, n9}
D[q,c] <- t // q1 = t
if(t not in Q) // Q = {q0, q1} , workList = [q1]
add t to Q and workList
闭包的计算~基于深度优先算法
参考数据结构,高一凡的代码实现。
/* ε-closure: 基于深度优先遍历的算法 */
set closure = {};
void eps_closure(x){
closure += {x}; // 集合的加法, 并
foreach(y: x --ε--> y){ // y 是 x 通过 ε 转换到的 y。
if(!visited(y)){ // 如果 y 还没有访问过,就访问 y
eps_closure(y);
}
}
}
闭包的计算~基于宽度优先算法
参考数据结构,高一凡的代码实现。
/* ε-closure: 基于宽度优先遍历的算法 */
set closure = {};
Q = []; // quenu 基于队列的概念,
void eps_closure(x) =
Q = [x];
while(Q not empty)
q <- deQueue(Q)
closure += q
foreach(y: q --ε--> y) // 将所有的从 Q 开始可以走到的 y 都加到 Q 里
if(!visited(y))
enQueue(Q,y)
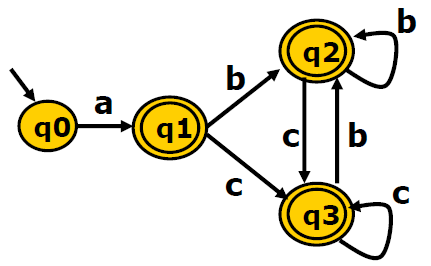
DFA的最小化:Hopcroft最小化算法
上图的DFA,如果他们都是输入,或者都是结束状态,就可以考虑合并的问题。例如q2与q3都是结束状态(两个圈),并且他俩还互相转换,合并后用一个状态来表示:

q1和q4再合并:

因为这样的DFA状态转换图在后面都要用数据结构边和结点来表示,越简单对后面的实现越有利。
// 基于等价类的思想
split(S)
foreach (character c)
if (c can split S)
split S into T1, …, Tk
hopcroft ()
split all nodes into N, A
while (set is still changes)
split(S)
DFA的代码表示

从概念上来说,DFA就是一个有向图,在数据结构中,有向图的具体实现有以下几种方式:
- 转移表(类似于邻接矩阵)
- 哈希表
- 跳转表
具体使用哪种数据结构需要结合实际,在空间和时间上作取舍。
转移表
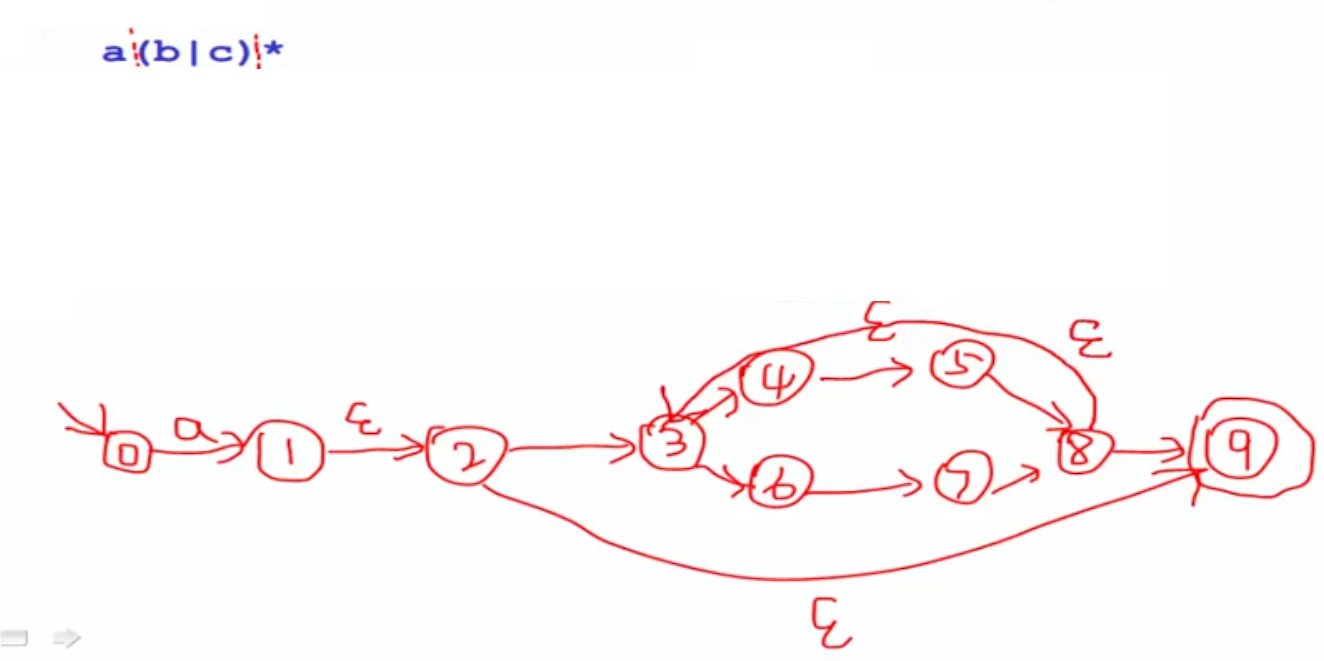
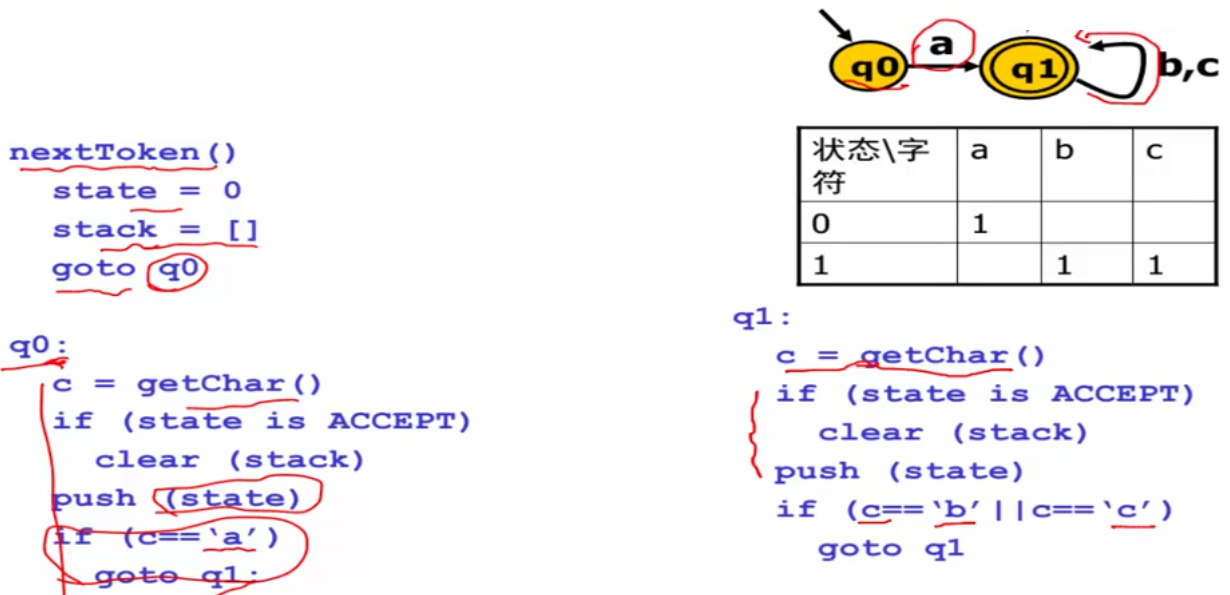
RE:a(b|c)*
DFA:

可以把确定有限状态自动机编码成下表:

表行是所有的字符,表列是所有的状态q0、q1(这里把q省掉了,直接用下标表示)。上图的1表示下一个跳转的状态,1代表跳转到q1。
举例解释下:

q0可接收“a”这个字符。
c语言可用二维数组存储:M、N表示行列数。

有了转移表,我们还有有个驱动代码,驱动代码可以读取我们输入的字符串,然后通过转移表去判断能否被接收,如果能被转移表接收也就表示能被DFA接收。
最长分配问题
举个例子:ifif(…),会将ifif识别为标识符而不是关键字。需要“往前看”。
跳转表
基本实现:把每个状态变成一段代码,把状态之间边的转移变成label,每段代码负责识别当前状态上所能识别的字符。
参考文献:
编译原理 华保健 高清课程