规格化数
在计算机中,借用数学中科学记数法概念,将小数记为1.xx*10^xx 的形式,同时小数点左侧的数值恒定为1。——起名叫做规格化数。
浮点数表示
计算机中采用IEEE 754标准,具体存储和表示可参考:MIPS汇编语言学习笔记06:print a float 中的讲解视频。
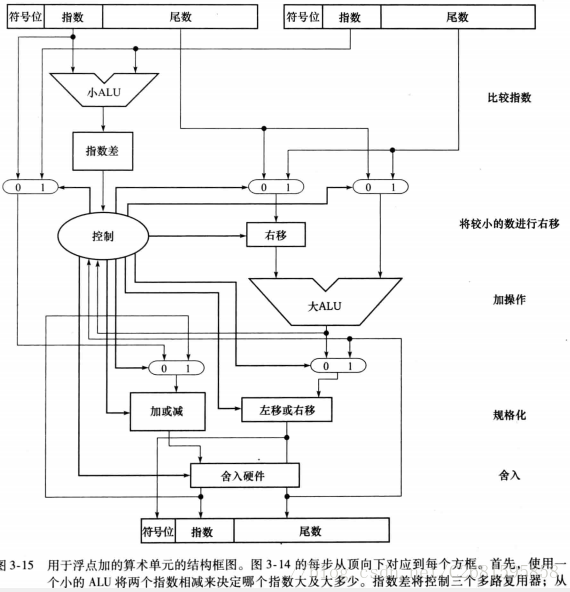
浮点数硬件实现——加法
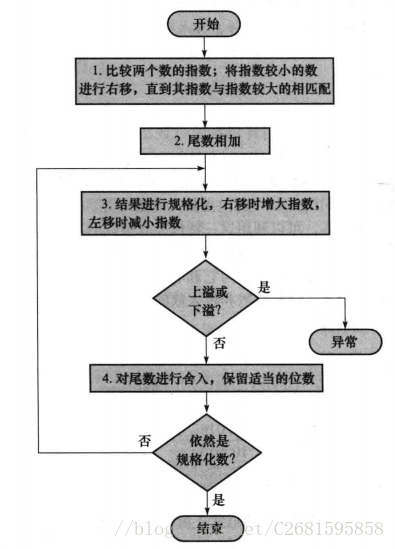
流程图:
- 第一步当中应该是将数的尾数部分右移,这样尾数就会减小,为了保证数字正确,指数部分必须增大,这样就刚好达到我们的目的。
- 第四步,判断是否是规格化数,这是因为对尾数进行四舍五入的时候,可能发生不测,进而需要再次规格化。
浮点数硬件实现——乘法
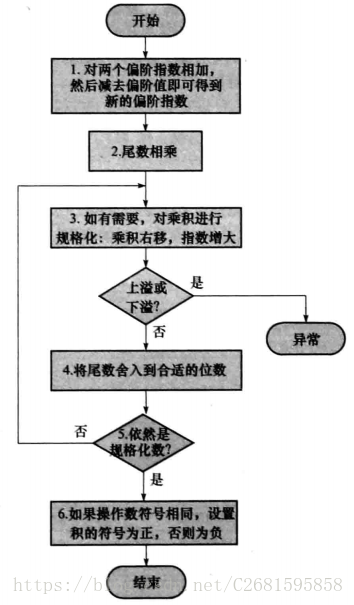
流程图:
- 第一步中要减去一个偏阶值,是因为当两个指数相加时,偏阶值加了两次。
- 其他步骤和加法相似,第五步,符号要根据两个源操作数来确定,同号为正,异号为负。
MIPS汇编中的浮点数指令
- MIPS有如下指令来支持IEEE754标准:
- 浮点单精度加(add.s)和双精度加(add.d)。
- 浮点单精度减(sub.s)和双精度减(sub.d)。
- 浮点单精度乘(mul.s)和双精度乘(mul.d)。
- 浮点单精度除(div.s)和双精度除(div.d)。
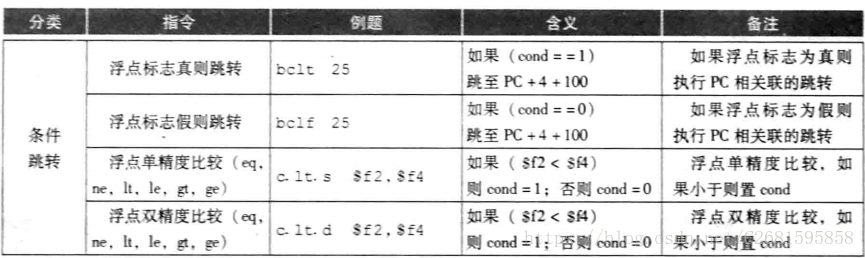
- 浮点单精度比较(c.x.s)和双精度比较(c.x.d)。
Ps:其中x指的是,等于(eq),不等于(neq),小于(lt),小于等于(le),大于(gt),大于等于(ge)。 - 浮点比较为真,跳转(bclt)和浮点比较为假,跳转(bclt):
- MIPS寄存器的规划,参考:MIPS汇编语言学习笔记30:浮点数(小数)运算
- 浮点存取指令:lwc1,swc1。
- 双精度寄存器是一组单精度寄存器的偶数-奇数对,并使用偶数寄存器作为名称,列如,单精度 $f2和 $f3作为双精度$f2。
浮点数算法精确性规定
IEEE754在计算中间值的时候,会在右边多保留2位,分别称为保护位和舍入位。
- 保护位:在浮点计算中,右边多保留的两位中的第一位。
- 舍入位:在浮点计算中,右边多保留的两位中的第二位。
就是说比起规格化数的话,他会在右边多出两位,以提高最终结果的精度。
参考文献:https://blog.csdn.net/c2681595858/article/details/80158863