本文已收录到:MIPS架构CPU设计 专题
CPU寄存器中存储的是补码,那么我们接下来就会遇到一个问题。
MIPS中除法指令
MIPS中共有两条除法指令,分别是 div 和 divu ,分别用于有符号数除法运算和无符号数除法运算。具体可参考:https://blog.csdn.net/leishangwen/article/details/39079817
在CPU中寄存器中,所有的数值都是补码,关于补码/原码转换,可以使用 原码,反码,补码相互转换在线计算器 小工具。
修改译码阶段
id.v:
... ...
6'b011010: begin
alusel_o <= `EXE_RES_ARITHMETIC;
aluop_o <= `EXE_DIV_OP;
wreg_o <= 1'b0;
reg1_read_o <= 1'b1;
reg2_read_o <= 1'b1;
instVaild <= `InstVaild;
end
6'b011011: begin
alusel_o <= `EXE_RES_ARITHMETIC;
aluop_o <= `EXE_DIVU_OP;
wreg_o <= 1'b0;
reg1_read_o <= 1'b1;
reg2_read_o <= 1'b1;
instVaild <= `InstVaild;
end
... ...
defines.v:
`define EXE_DIV_OP 8'b10010011 `define EXE_DIVU_OP 8'b10010100
使用补码除法运算?使用原码除法运算?
除法运算,-10/5这种情况允许吗?在div和divu指令中如何处理,结果是什么?可以通过MARS软件测试。
.text main: li $t0, -10 li $t1, 10 li $t2, 5 li $t3, -5 # -10/5 = -2 div $t0, $t2 # ffff fffe(补码) # -10/-5 = 2 div $t0, $t3 # 0000 0002(补码) # 10/5 = 2 div $t1, $t2 # 0000 0002(补码) # 10/-5 = -2 div $t1, $t3 # ffff fffe(补码)
补码原码相互转换
关于补码的知识可以参考:补码的来历,补码的优势
补码转换原码
DIV指令下(有符号数):
- 被除数/除数为正数:补码等于其原码本身。
- 被除数/除数为负数,则转换成原码,所有位按位取反,再在最低位加1。
//补码转换为原码 div_dividend <= (reg1_i[31] == 1'b1) ? (~reg1_i + 1) : reg1_i; div_divisor <= (reg2_i[31] == 1'b1) ? (~reg2_i + 1) : reg2_i;
原码转为补码
DIV指令下,将商和余数转回为补码:
- 对于正数:补码就是原码本身。
- 对于负数:原码的符号位不变,其余位按位取反,再在最低位加1。
assign div_quotient = ((aluop_i == `EXE_DIV_OP) && (reg1_i[31] ^ reg2_i[31] == 1'b1)) ? {1'b1, (~div_quo_o[30:0] + 1)} : div_quo_o;
assign div_remainder = ((aluop_i == `EXE_DIV_OP) && (reg1_i[31] == 1'b1)) ? {1'b1, (~div_rem_o[30:0] + 1)} : div_rem_o;
原码除法运算——试商法
可参考下面的pdf课件,来源:北京大学《计算机组成》课程
除法模块
首先我们先明确一点:我们讨论和实现的除法器都是基于试商法+原码除法器的。我们不考虑补码除法器和其他方式(如:查表法)实现的除法器。
组合逻辑实现
div.v模块使用组合逻辑实现了有符号数的除法:
.text main: li $t0, -10 li $t1, 10 li $t2, 5 li $t3, -5 # 10/5 = 2 div $t1, $t2 # 0000 0002(补码)
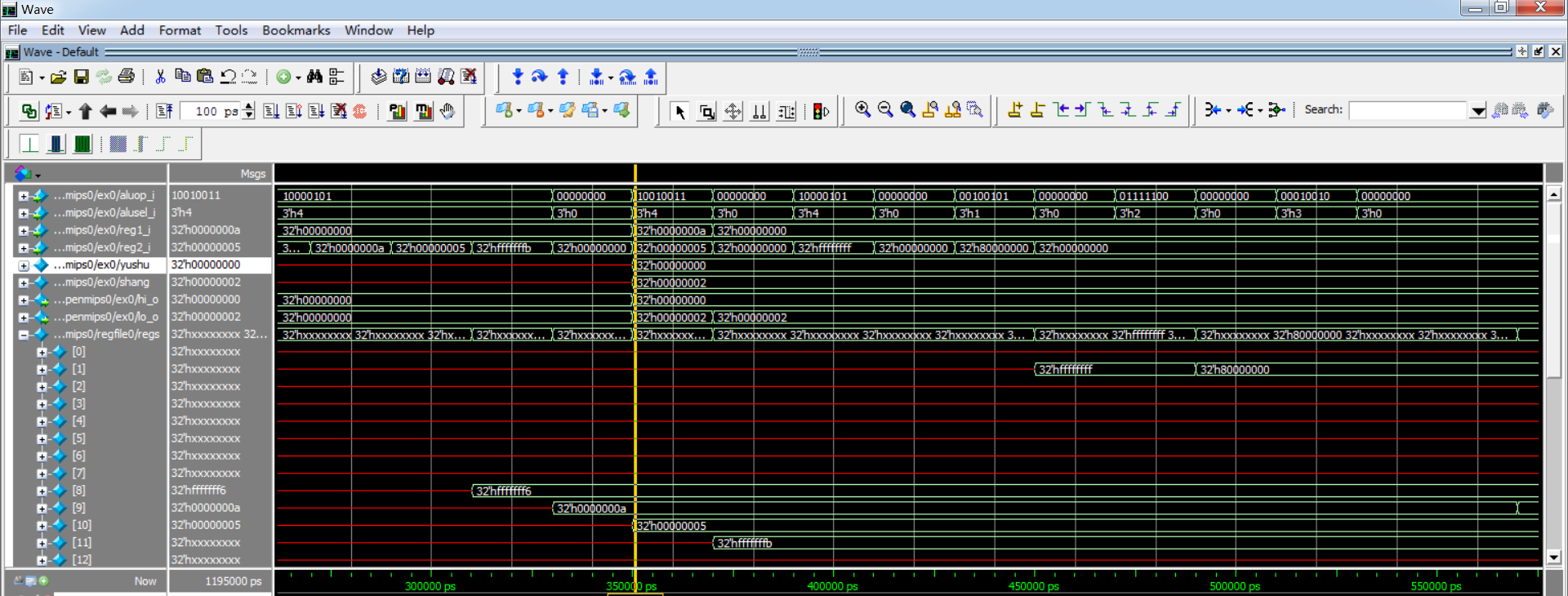
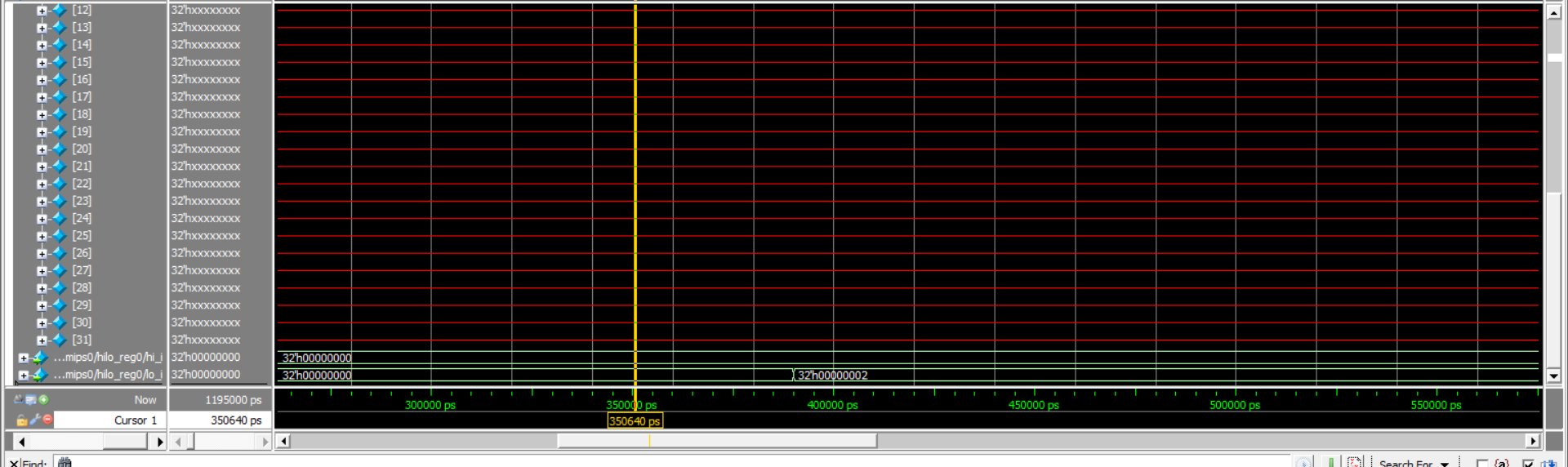
.text main: li $t0, -10 li $t2, 5 # -10/5 = -2 div $t0, $t2
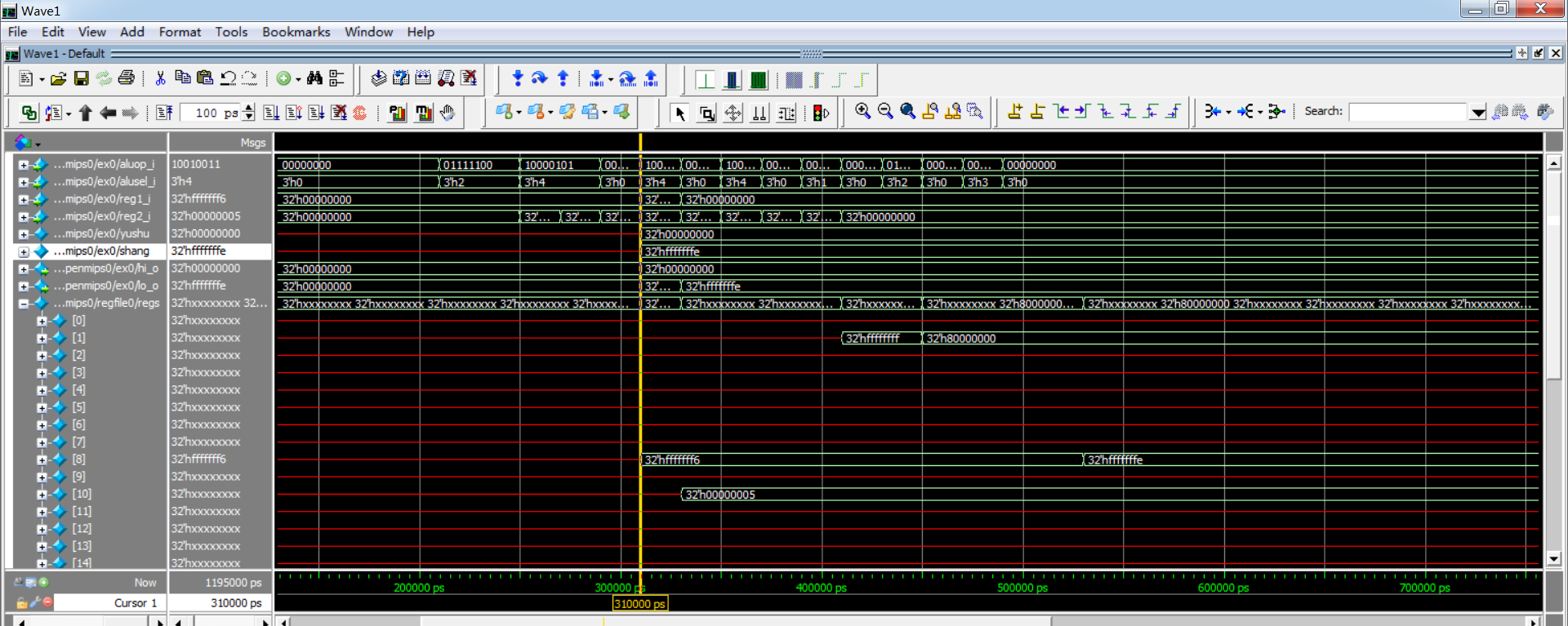
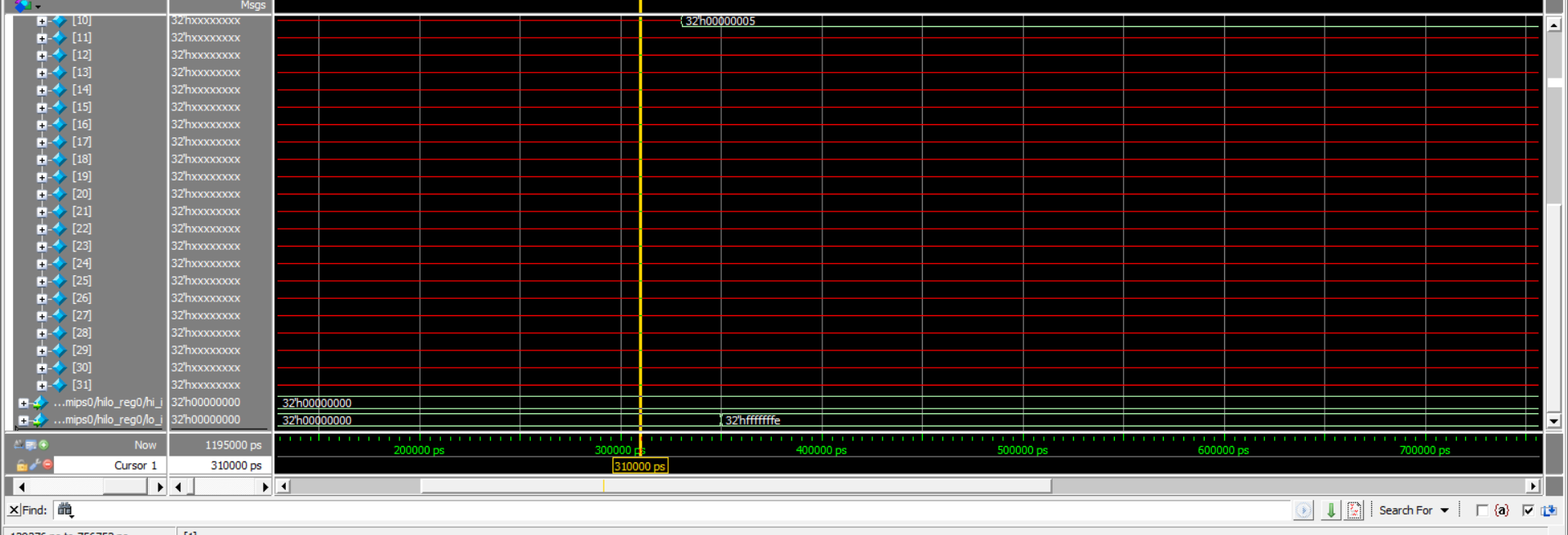
.text main: li $t0, -10 li $t2, -5 # -10/-5 = 2 div $t0, $t2

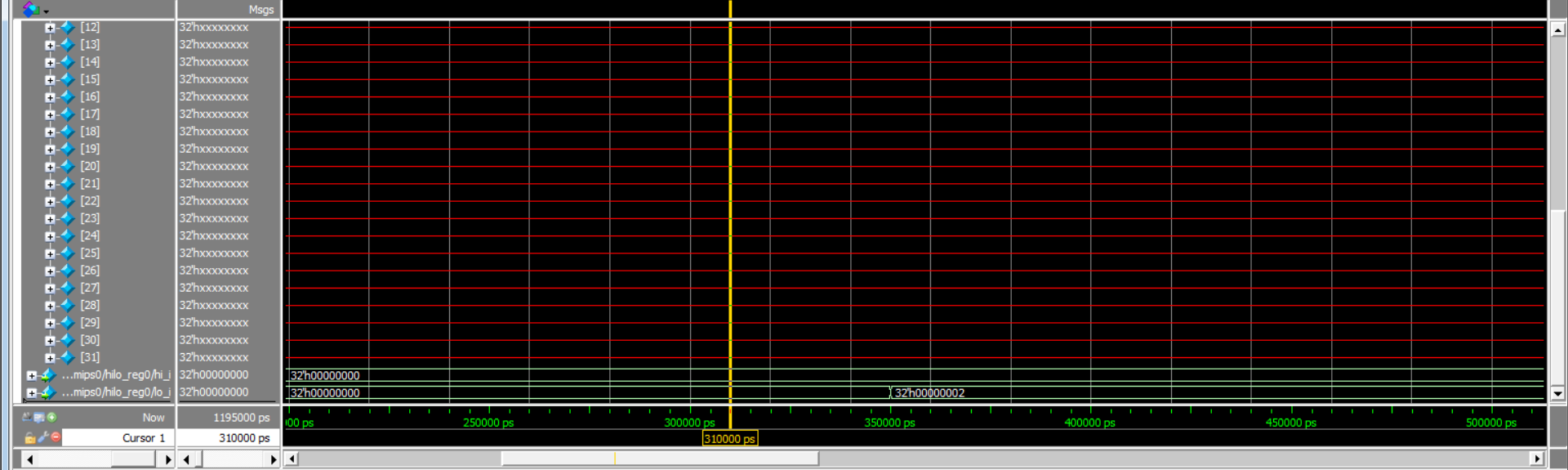
.text main: li $t1, 10 li $t3, -5 # 10/-5 = -2 div $t1, $t3 # ffff fffe(补码)
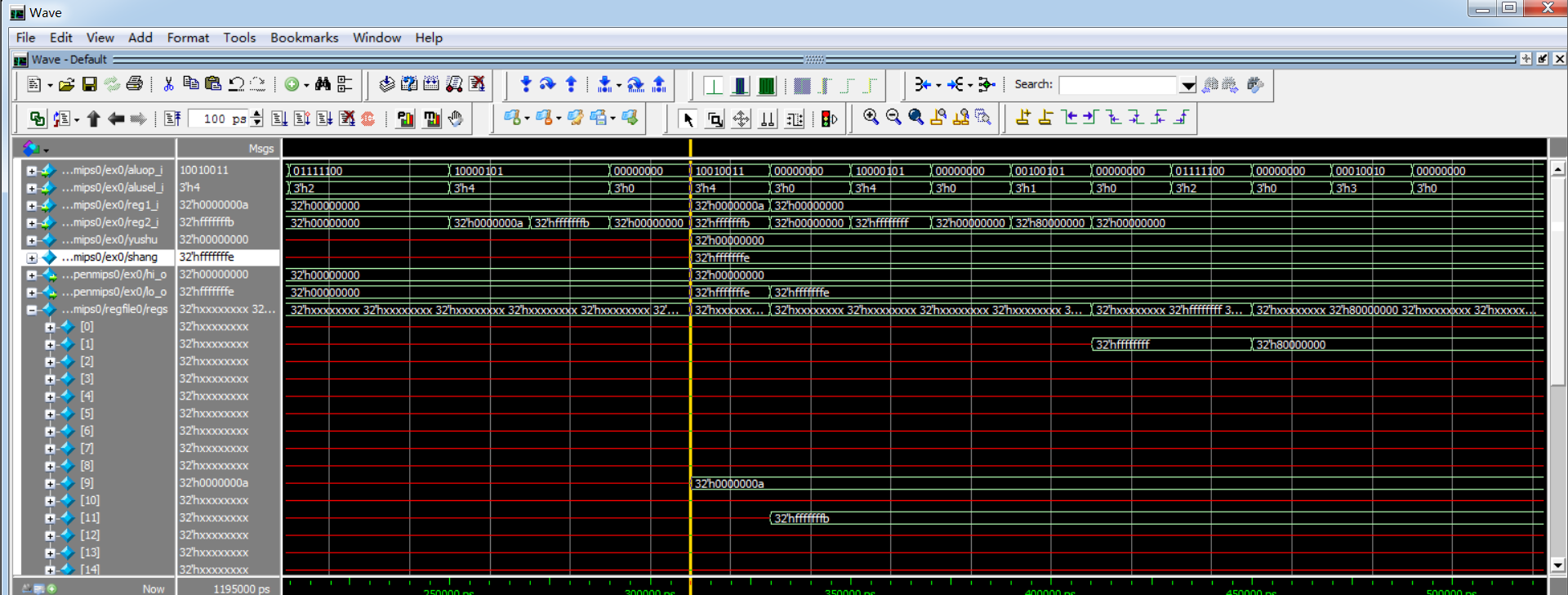
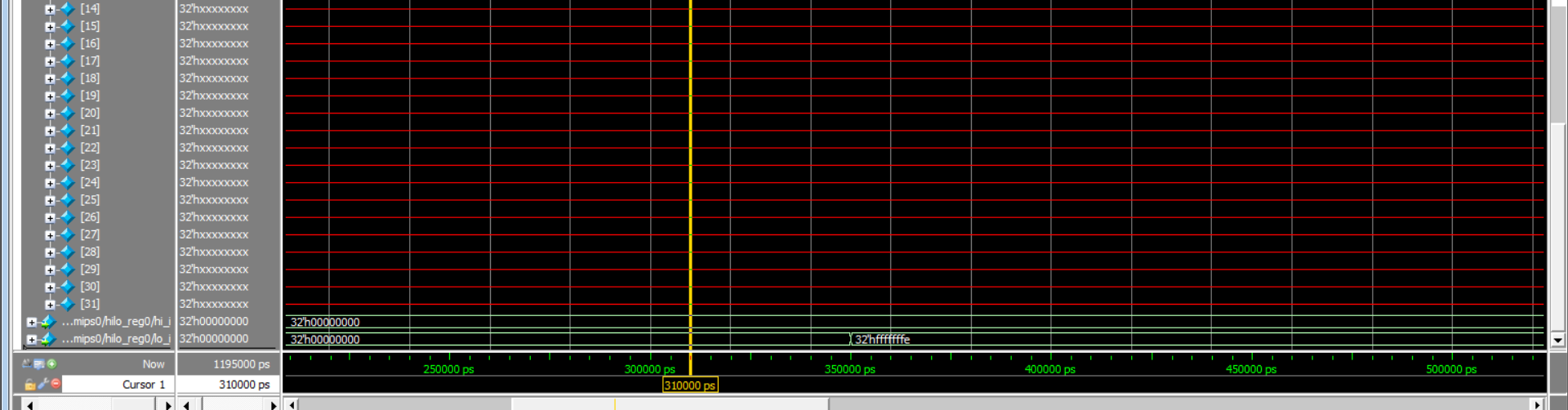
但是,使用组合逻辑出现了很多问题,具体可以看下视频中当时记录的情况:
时序逻辑实现
div_fsm.v 是使用时序逻辑+自动机实现的无符号基于试商法的除法模块。
执行阶段实现
执行模块的实现,我们以有符号数为例介绍。
首先,CPU中存储的数一定是补码形式的,我们前面的除法 div_fsm.v 模块输入端的被除数和除数都是基于原码形式实现的。
所以在执行阶段、输出到div_fsm模块之前需要先将被除数和除数转化为原码形式。
从div_fsm.v 模块输出到ex执行阶段的被输出和除数均为原码形式,我们接下来需要对其进行处理。具体有两步:
- 添加符号,即商和余数负号。
- 将原码转换为补码,以便于存储在寄存器中。
CPU中,商和余数的负号如何确定:CPU中有符号数除法,余数和商的符号取决于什么?
代码:
`EXE_DIV_OP: begin
// 除法准备好了
if (div_ready_i == 1'b1) begin
// 除法模块开始运行
// 符号是正号
if ((reg1_i[31] == 1'b0 && reg2_i[31] == 1'b0) || (reg1_i[31] == 1'b1 && reg2_i[31] == 1'b1)) begin
//补码转换为原码
div_dividend <= (reg1_i[31] == 1'b1) ? (~reg1_i + 1) : reg1_i;
div_divisor <= (reg2_i[31] == 1'b1) ? (~reg2_i + 1) : reg2_i;
// 符号是负号
end else if ((reg1_i[31] == 1'b1 && reg2_i[31] == 1'b0) || (reg1_i[31] == 1'b0 && reg2_i[31] == 1'b1)) begin
//补码转换为原码
div_dividend <= (reg1_i[31] == 1'b1) ? (~reg1_i + 1) : reg1_i;
div_divisor <= (reg2_i[31] == 1'b1) ? (~reg2_i + 1) : reg2_i;
end
div_start_o <= 1'b1; // div模块使能信号
div_data1_o <= div_dividend; // 被除数传到除法模块
div_data2_o <= div_divisor; // 除数传到除法模块
suspendsignal_from_div <= 1'b1;
// 除法结束
end else if (div_cnt_i == 1'b1) begin
// 除法模块运算完成
// 添加符号、原码转为补码判断和处理:
// 1. 商、余数符号为判断可参考:https://gaozhiyuan.net/digital-electronics/2s-complement.html
// 1. 如果结果位是正数,则本身就是补码,因为正数的补码和原码相同。
// 3. 如果结果位是负数,则其所有位按位取反+1后就是其补码。eg:2原码为 0000 0010,-2补码为 1111 1110
if (reg1_i[31] ^ reg2_i[31] == 1'b0) begin
shang <= div_shang_i;
end else if (reg1_i[31] ^ reg2_i[31] == 1'b1) begin
shang <= (~div_shang_i + 1);
end
if (reg1_i[31] == 1'b0) begin
yushu <= div_yushu_i;
end else if (reg1_i[31] == 1'b1) begin
yushu <= (~div_yushu_i + 1);
end
suspendsignal_from_div <= 1'b0;
end
end
章节测试
inst_rom.asm:
inst_rom.om: file format elf32-tradbigmips Disassembly of section .text: 00000000 <_start>: 0: 3402ffff li v0,0xffff 4: 00021400 sll v0,v0,0x10 8: 3442fff1 ori v0,v0,0xfff1 c: 34030011 li v1,0x11 10: 0043001a div zero,v0,v1 14: 0043001b divu zero,v0,v1 18: 0062001a div zero,v1,v0 Disassembly of section .reginfo: 00000000 <_ram_end-0x20>: 0: 0000000c syscall ...
仿真波形图:

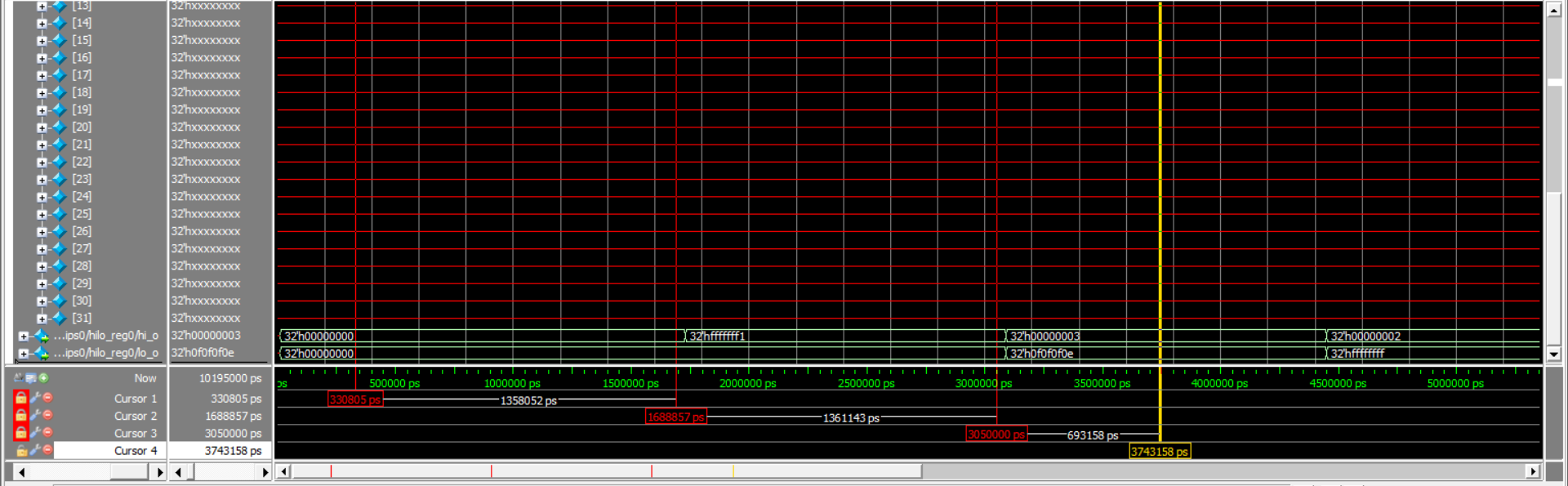
本章代码
https://github.com/gzhy5111/cpu
参考文献:
北京大学《计算机组成》课程 陆俊林
https://www.codeprj.com/blog/735d581.html
https://blog.csdn.net/qq_39507748/article/details/108909681