“农场里有群火鸡,农场主每天中午十一点来喂食。火鸡中有位科学家观察了近一年无例外后宣布发现了宇宙一个伟大定律:“每天上午十一点,会有食物降临。”感恩节早晨,它向火鸡们公布了这个定律,但这天上午十一点食物没有降临,农场主将它们捉去杀掉,把它们变成了食物。” --罗素的火鸡
# 科学计算模块
import numpy as np
import pandas as pd
# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt
# 自定义模块
from ML_basic_function import *
在Lesson 0中我们曾说,模型评估指标是用于评估模型效果好坏的数值指标,例如SSE就是评估回归类模型拟合效果的指标。但是否是评估指标好的模型就一定能用呢?其实并不一定。这里会涉及到一个关于评估指标可信度问题、或者说了解模型真实性能的重要命题。
其实,要了解模型的性能其实并不简单,固然我们会使用某些指标去进行模型评估,但其实指标也只是我们了解模型性能的途径而不是模型性能本身。而要真实、深刻的评判模型性能,就必须首先了解机器学习的建模目标,并在此基础之上熟悉我们判断模型是否能够完成目标的一些方法,当然,只有真实了解的模型性能,我们才能进一步考虑如何提升模型性能。因此,在正式讲解模型优化方法之前,我们需要花些时间讨论机器学习算法的建模目标、机器学习算法为了能够达到目标的一般思路,以及评估模型性能的手段,也就是模型评估指标。
无论是机器学习还是传统的统计分析模型,核心使命就是探索数字规律,而有监督学习则是希望在探索数字规律的基础上进一步对未来进行预测,当然,在数字的世界,这个预测未来,也就是预测未来某项事件的某项数值指标,如某地区未来患病人次、具备某种数字特征的图片上的动物是哪一类,此处的未来也并非指绝对意义上的以后的时间,而是在模型训练阶段暂时未接触到的数据。正是因为模型有了在未知标签情况下进行预判的能力,有监督学习才有了存在的价值,但我们知道,基本上所有的模型,都只能从以往的历史经验当中进行学习,也就是在以往的、已经知道的数据集上进行训练(如上述利用已知数据集进行模型训练,如利用过往股票数据训练时间序列模型),这里的核心矛盾在于,在以往的数据中提取出来的经验(也就是模型),怎么证明能够在接下来的数据中也具备一定的预测能力呢?或者说,要怎么训练模型,才能让模型在未知的数据集上也拥有良好的表现呢?
目的相同,但在具体的实现方法上,传统的数理统计分析建模和机器学习采用了不同的解决方案。
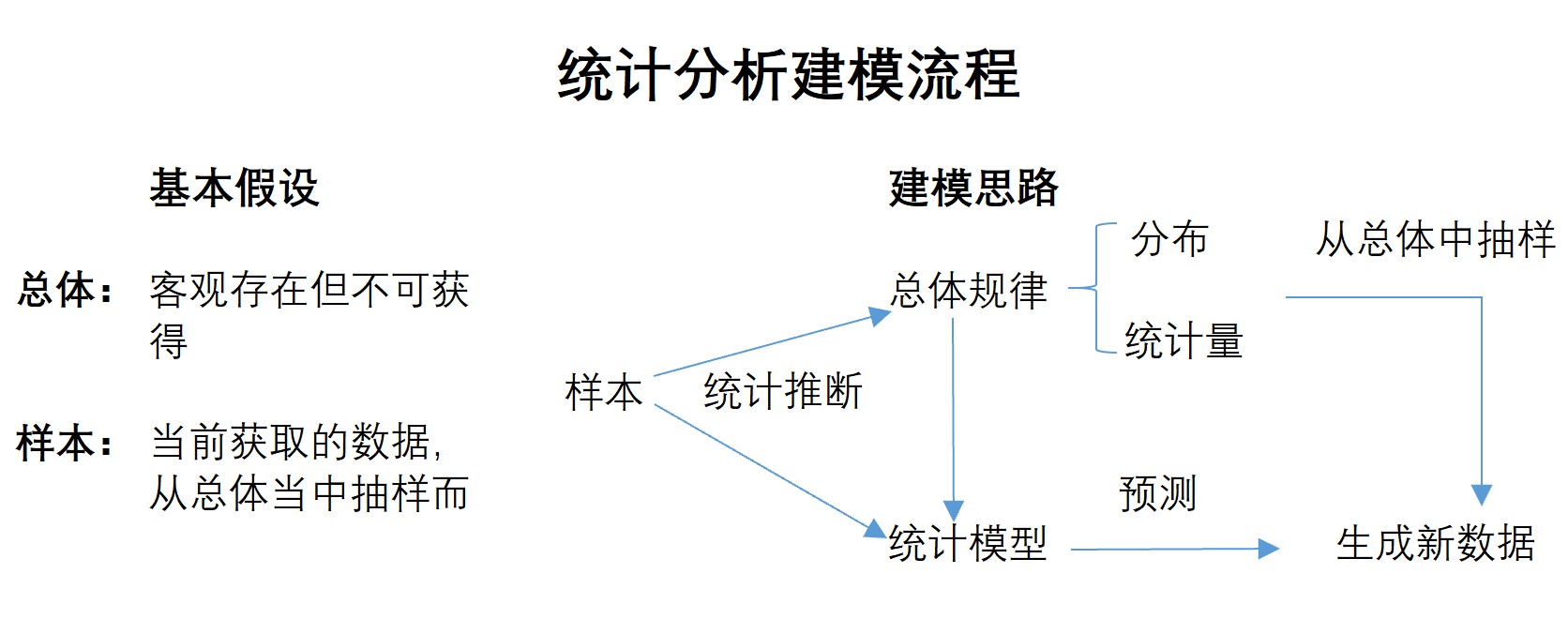
首先,在统计分析领域,我们会假设现在的数据和未来的数据其实都属于某个存在但不可获得的总体,也就是说,现在和未来的数据都是从某个总体中抽样而来的,都是这个总体的样本。而正式因为这些数据属于同一个总体,因此具备某些相同的规律,而现在挖掘到的数据规律也就在某些程度上可以应用到未来的数据当中去,不过呢,不同抽样的样本之间也会有个体之间的区别,另外模型本身也无法完全捕获规律,而这些就是误差的来源。
虽然样本和总体的概念是统计学概念,但样本和总体的概念所假设的前后数据的“局部规律一致性”,却是所有机器学习建模的基础。试想一下,如果获取到的数据前后描绘的不是一件事情,那么模型训练也就毫无价值(比如拿着A股走势预测的时间序列预测某地区下个季度患病人次)。因此,无论是机器学习所强调的从业务角度出发,要确保前后数据描述的一致性,还是统计分析所强调的样本和总体的概念,都是建模的基础。
在有了假设基础之后,统计分析就会利用一系列的数学方法和数理统计工具去推导总体的基本规律,也就是变量的分布规律和一些统计量的取值,由于这个过程是通过已知的样本去推断未知的总体,因此会有大量的“估计”和“检验”,在确定了总体的基本分布规律之后,才能够进一步使用统计分析模型构建模型(这也就是为什么在数理统计分析领域,构建线性回归模型需要先进行一系列的检验和变换的原因),当然,这些模型都是在总体规律基础之上、根据样本具体的数值进行的建模,我们自然有理由相信这些模型对接下来仍然是从总体中抽样而来的样本还是会具备一定的预测能力,这也就是我们对统计分析模型“信心”的来源。简单来说,就是我们通过样本推断总体的规律,然后结合总体的规律和样本的数值构建模型,由于模型也描绘了总体规律,所以模型对接下来从总体当中抽样而来的数据也会有不错的预测效果,这个过程我们可以通过下图来进行表示。

而对于机器学习来说,并没有借助“样本-总体”的基本理论,而是模拟了一种后验的流程来判别模型有效性,将数据进行切分。前面说到,我们假设前后获取的数据拥有规律一致性,但数据彼此之间又略有不同,为了能够在捕捉规律的同时又能考虑到“略有不同”所带来的误差,机器学习会把当前能获取到的数据划分成训练集(trainSet)和测试集(testSet),在训练集上构建模型,然后带入测试集的数据,观测在测试集上模型预测结果和真实结果之间的差异。这个过程其实就是在模拟获取到真实数据之后模型预测的情况,此前说到,模型能够在未知标签的数据集上进行预测,就是模型的核心价值,此时的测试集就是用于模拟未来的未知标签的数据集。如果模型能够在测试集上有不错的预测效果,我们就“简单粗暴”的认为模型可以在真实的未来获取的未知数据集上有不错的表现。其一般过程可以由下图表示。

虽然对比起数理统计分析,机器学习的证明模型有效性的过程更加“简单”,毕竟只要一次“模拟”成功,我们就认为模型对未来的数据也拥有判别效力,但这种“简单”的处理方式却非常实用,可以说,这是一种经过长期实践被证明的行之有效的方法。这也是为什么机器学习很多时候也被认为是实证类的方法,而在以后的学习中,我们也将了解到,机器学习有很多方法都是“经验总结的结果”。相比数理统计分析,确实没有“那么严谨”,但更易于理解的理论和更通用的方法,却使得机器学习可以在更为广泛的应用场景中发挥作用。(当然,负面影响却是,机器学习在曾经的很长一段时间内并不是主流的算法。)
据此,我们称模型在训练集上误差称为训练误差,在测试集上的误差称为泛化误差,不过毕竟在测试集上进行测试还只是模拟演习,我们采用模型的泛化能力来描述模型在未知数据上的判别能力,当然泛化能力无法准确衡量(未知的数据还未到来,到来的数据都变成了已知数据),我们只能通过模型在训练集和测试集上的表现,判别模型泛化能力,当然,就像此前说的一样,最基本的,我们会通过模型在测试集上的表现来判断模型的泛化能力。
接下来,我们就尝试通过数据集切分来执行更加可信的机器学习建模流程。首先是对数据集进行切分。一般来说,为了避免数据集上下顺序对数据规律的影响,我们会考虑对数据集进行随机切分,其中70%-80%作为训练集、20%-30%作为测试集。此处我们先考虑构建一个数据切分函数,用于训练集和测试集的切分:
在NumPy中,我们可以非常便捷的通过调用np.random.shuffle函数来进行二维数组按行重排的相关操作,而二维数组也就是结构化数据的一般表示形式,因此我们可以使用该函数进行数据集乱序排列。并且我们可以通过设置随机数种子,来复现这个乱序的过程,这将极大程度有助于当需要对多个序列进行乱序排列时的代码简化。
A = np.arange(10).reshape(5, 2)
A
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
B = np.arange(0, 10, 2).reshape(-1, 1)
B
array([[0],
[2],
[4],
[6],
[8]])
np.random.seed(24)
np.random.shuffle(A)
A
array([[8, 9],
[2, 3],
[0, 1],
[6, 7],
[4, 5]])
B
array([[0],
[2],
[4],
[6],
[8]])
np.random.seed(24)
np.random.shuffle(B)
B
array([[8],
[2],
[0],
[6],
[4]])
此外,我们可以通过vsplit函数进行数组的按行切分,也就相当于split(axis=0)。
A
array([[8, 9],
[2, 3],
[0, 1],
[6, 7],
[4, 5]])
# 从行索引的第二、三元素之间切开
np.vsplit(A,[2, ])
[array([[8, 9],
[2, 3]]),
array([[0, 1],
[6, 7],
[4, 5]])]
基于上述函数,我们可以非常简单的构建一个数据集切分函数:
def array_split(features, labels, rate=0.7, random_state=24):
"""
训练集和测试集切分函数
:param features: 输入的特征张量
:param labels:输入的标签张量
:param rate:训练集占所有数据的比例
:random_state:随机数种子值
:return Xtrain, Xtest, ytrain, ytest:返回特征张量的训练集、测试集,以及标签张量的训练集、测试集
"""
np.random.seed(random_state)
np.random.shuffle(features) # 对特征进行切分
np.random.seed(random_state)
np.random.shuffle(labels) # 按照相同方式对标签进行切分
num_input = len(labels) # 总数据量
split_indices = int(num_input * rate) # 数据集划分的标记指标
Xtrain, Xtest = np.vsplit(features, [split_indices, ])
ytrain, ytest = np.vsplit(labels, [split_indices, ])
return Xtrain, Xtest, ytrain, ytest
一般来说,训练集和测试集可以按照8:2或7:3比例进行划分。在进行数据划分的过程中,如果测试集划分数据过多,参与模型训练的数据就会相应减少,而训练数据不足则会导致模型无法正常训练、损失函数无法收敛、模型过拟合等问题,但如果反过来测试集划分数据过少,则无法代表一般数据情况测试模型是否对未知数据也有很好的预测作用。因此,根据经验,我们一般来说会按照8:2或7:3比例进行划分。
看到这里,相信肯定有小伙伴觉得根据所谓的“经验”来定数据集划分比例不太严谨,有没有一种方法能够“精准”的确定什么划分比例最佳呢?例如通过类似最小二乘法来计算划分比例?
值得一提的是,在机器学习领域,充斥着大量的“经验之谈”或者“约定俗成”的规则,一方面这些经验为建模提供了诸多便捷、也节省了很多算力,但另一方面,通过经验来决定影响模型效果的一些“超参数”取值的不严谨的做法,也被数理统计分析流派所诟病。
接下来,测试函数性能
f = np.arange(10).reshape(-1, 1) # 创建特征0-9
f
array([[0],
[1],
[2],
[3],
[4],
[5],
[6],
[7],
[8],
[9]])
l = np.arange(1, 11).reshape(-1, 1) # 创建标签1-10,保持和特征+1的关系
l
array([[ 1],
[ 2],
[ 3],
[ 4],
[ 5],
[ 6],
[ 7],
[ 8],
[ 9],
[10]])
array_split(f, l)
(array([[9],
[4],
[8],
[7],
[5],
[6],
[1]]),
array([[0],
[3],
[2]]),
array([[10],
[ 5],
[ 9],
[ 8],
[ 6],
[ 7],
[ 2]]),
array([[1],
[4],
[3]]))
根据机器学习结果可信度理论,我们构建一个在训练集上训练、在测试集上测试的完整的线性回归实现流程。
# 设置随机数种子
np.random.seed(24)
# 扰动项取值为0.01
features, labels = arrayGenReg(delta=0.01)
# 数据切分
Xtrain, Xtest, ytrain, ytest = array_split(features, labels)
最小二乘法求解公式:$$\hat w = (X^TX)^{-1}X^Ty$$
w = np.linalg.inv(Xtrain.T.dot(Xtrain)).dot(Xtrain.T).dot(ytrain)
w
array([[ 1.99976073],
[-0.99986178],
[ 0.99934303]])
在大多数情况下,所谓训练模型,都是训练得出模型的一组参数。
然后即可在测试集上计算模型评估指标:
SSELoss(Xtest, w, ytest)
array([[0.02725208]])
至此,我们即完成了模型在训练集上训练得出参数,然后运行测试集观察结果的全过程。由于数据情况较为简单,因此模型效果较好。
但如果测试集效果不好,我们能否因此对模型进行调整的呢?如果测试集真的完全不参与建模,那么根据测试集反馈结果调整模型是否算测试集间接参与建模?如果测试集不能间接参与建模,那测试集的提供的模型结果反馈又有什么作用呢?这就是所谓的,测试集悖论。
我们已经知道,机器学习模型主要通过模型在测试集上的运行效果来判断模型好坏,测试集相当于是“高考”,而此前的模型训练都相当于是在练习,但怎么样的练习才能有效的提高高考成绩,这里就存在一个“悖论”,那就是练习是为了高考,而在高考前我们永远不知道练习是否有效,那高考对于练习的核心指导意义何在?在机器学习领域,严格意义上的测试集是不能参与建模的,此处不能参与建模,不仅是指在训练模型时不能带入测试集进行训练,更是指当模型训练完成之后、观察模型在测试集上的运行结果后,也不能据此再进行模型修改(比如增加神经网络层数),后面我们会提到,把数据带入模型训练是影响模型参数,而根据模型运行结果再进行模型结构调整,实际上是修改了模型超参数,不管是修改参数还是超参数,都是影响了模型建模过程,都相当于是带入进行了建模。是的,如果通过观察测试集结果再调整模型结构,也相当于是带入测试集数据进行训练,而严格意义上的测试集,是不能带入模型训练的。(这是一个有点绕的“悖论”....)
但是,还记得我们此前说的,机器学习建模的核心目标就是提升模型的泛化能力么?而泛化能力指的是在模型未知数据集(没带入进行训练的数据集)上的表现,虽然测试集只能测一次,但我们还是希望有机会能把模型带入未知数据集进行测试,此时我们就需要一类新的数据集——验证集。验证集在模型训练阶段不会带入模型进行训练,但当模型训练结束之后,我们会把模型带入验证集进行计算,通过观测验证集上模型运行结果,判断模型是否要进行调整,验证集也会模型训练,只不过验证集训练的不是模型参数,而是模型超参数,关于模型参数和超参数的概念后面还会再详细讨论,当然,我们也可以把验证集看成是应对高考的“模拟考试”,通过“模拟考试”的考试结果来调整复习策略,从而更好的应对“高考”。总的来说,测试集是严格不能带入训练的数据集,在实际建模过程中我们可以先把测试集切分出来,然后“假装这个数据集不存在”,在剩余的数据集中划分训练集和验证集,把训练集带入模型进行运算,再把验证集放在训练好的模型中进行运行,观测运行结果,再进行模型调整。
总的来说,在模型训练和观测模型运行结果的过程总共涉及三类数据集,分别是训练集、验证集和测试集。不过由于测试集定位特殊,在一些不需要太严谨的场景下,有时也会混用验证集和测试集的概念,我们常常听到“测试集效果不好、重新调整模型”等等,都是混用了二者概念,由于以下是模拟练习过程,暂时不做测试集和验证集的区分。在不区分验证集和测试集的情况下,当数据集切分完成后,对于一个模型来说,我们能够获得两套模型运行结果,一个是训练集上模型效果,一个是测试集上模型效果,而这组结果,就将是整个模型优化的基础数据。
在某些场景下,测试集确实是严格不可知的,比如在线提交结果的数据竞赛。
除了训练集-测试集划分理论之外,交叉验证也可以衡量模型结果的可信度。
尽管通过训练集和测试集的划分,我们可以以不参与建模的测试集的结论来证明模型结果的可信度,但在很多实际场景中,数据集的随机切分本身也是影响模型泛化能力、影响测试集结果可信度的重要因素。此时,我们可以采用一种名为交叉验证的技术手段来进一步提升模型最终输出结果的可信度。交叉验证的基本思想非常简单,在我们不严格区分测试集的情况下,我们可以将数据集整体按照某个比例切分,然后进行循环验证。在所有的切分方法中,最基础也最常用的一种就是所谓的K-fold(K折)验证,也就是将数据集进行K份等比例划分,然后依次取出其中一份进行验证(测试)、剩下几份进行训练。例如,当我们使用10折验证时,数据集划分情况如下所示:
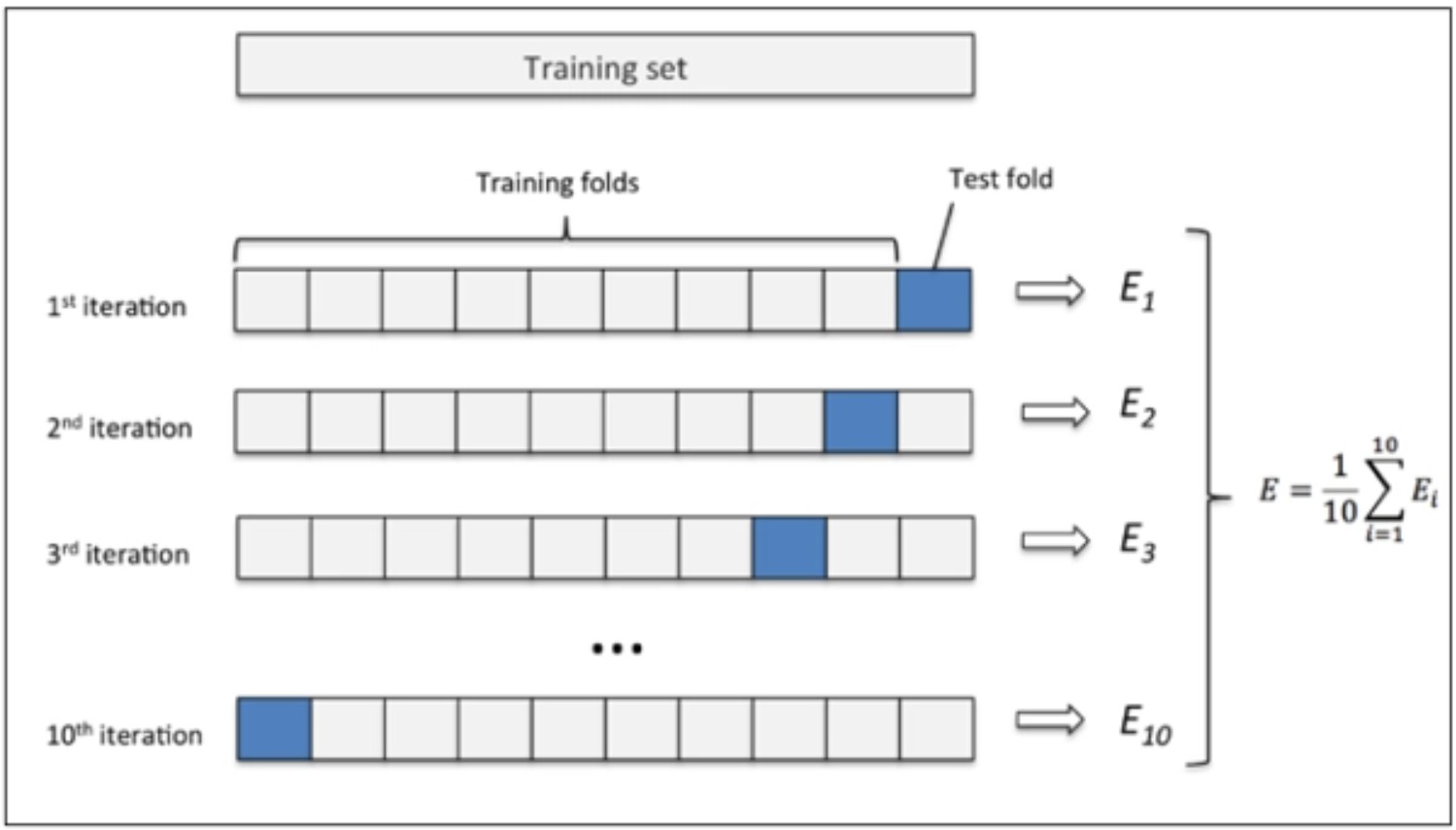
假设仍然是此前我们创建的数据集并且仍然采用SSE作为模型评估指标,则在进行十折验证时可以计算出十组SSE取值,最终我们可以对这十组结果进行均值计算,求得这组参数最终所对应的模型评估指标结果。不过此时我们需要在所有的数据集上进行训练,然后再进行交叉验证。
在十折的计算完成后,会产生十组参数,而训练出来的参数如果取均值是否合理又是一个问题。不能通过取均值的方法来获得交叉验证的参数。
不得不说,对于线性回归的交叉验证过程其实和训练集测试集划分理论略显冲突,如果缺少了测试集的后验过程,再训练集上再怎么训练,得出的结果都没有反馈调整的机会。其实从更加根本的角度来说,在机器学习理论体系中,一个更加严谨的做法,是先划分训练集和测试集,然后再在训练集上划分测试集,并且“训练集-测试集”划分方法用于进行模型参数训练,而“训练集-验证集”的划分方法主要用于进行模型超参数选取。此处由于我们尚未接触超参数相关概念,在此之前线性回归模型中的参数和此处的超参数不是一会事,在后面,交叉验证会进一步的指导模型超参数的选取。目前暂时先只介绍其基本思想。